A particle of mass 5 g is moving with a uniform speed of 3√2cm s−1 in the XY-plane along the line y=2√5 cm. The magnitude of its angular momentum about the origin in g-cm2s−1 is
zero
30
30√2
30√10
The correct Answer is:D
To find the angular momentum of a particle moving in the XY-plane about the origin, we can follow these steps:
Step 1: Identify the given values
- Mass of the particle, m=5g
- Speed of the particle, v=3√2cm/s
- The line of motion is given by y=2√5cm
Step 2: Determine the perpendicular distance from the origin to the line of motion
The line y=2√5 is horizontal, and the perpendicular distance from the origin (0, 0) to this line is simply the y-coordinate of the line:
- Perpendicular distance, d=2√5cm
Step 3: Use the formula for angular momentum
The formula for angular momentum L about the origin is given by:
L=m⋅v⋅d
Substituting the values we have:
L=5g⋅(3√2cm/s)⋅(2√5cm)
Step 4: Calculate the angular momentum
Now, we can calculate L:
L=5⋅3√2⋅2√5
L=5⋅6√10
L=30√10g-cm2/s
Step 5: Conclusion
The magnitude of the angular momentum about the origin is:
L=30√10g-cm2/s
Final Answer
The correct option is 30√10g-cm2/s.
---
- Mass of the particle, m=5g
- Speed of the particle, v=3√2cm/s
- The line of motion is given by y=2√5cm
The line y=2√5 is horizontal, and the perpendicular distance from the origin (0, 0) to this line is simply the y-coordinate of the line:
- Perpendicular distance, d=2√5cm
The formula for angular momentum L about the origin is given by:
L=m⋅v⋅d
Substituting the values we have:
L=5g⋅(3√2cm/s)⋅(2√5cm)
Now, we can calculate L:
L=5⋅3√2⋅2√5
L=5⋅6√10
L=30√10g-cm2/s
The magnitude of the angular momentum about the origin is:
L=30√10g-cm2/s
The correct option is 30√10g-cm2/s.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A particle of mass 5g is moving with a uniform speed of 3√2cm/s in the x−y plane along the line y=x+4. The magnitude of its angular momentum about the origin in gcm2/s is
View SolutionA particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA particle of mass 300 g is moving with a speed of 20 ms−1 along the straight line y = x - 4√2. The angular momentum of the particle about the origin is (where y & x are in metres)
View SolutionA particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle of mass m=3kg moves along a straight line 4y−3x=2 where x and y are in metre, with constant velocity v=5ms−1 the magnitude of angular momentum about the origin is
View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
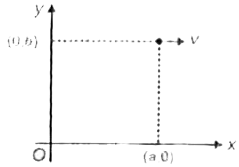
View SolutionA particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View Solution
