Electric charge q is distributed uniformly over a rod of length l. The rod is placed parallel to a long wire carrying a current i. The separation between the rod and the wire is a. The force needed to move the rod along its length with a uniform velocity v is
μ0iqv2πa
μ0iqv4πa
μ0iqvl2πa
μ0iqvl4πa
The correct Answer is:A
To solve the problem, we need to determine the force required to move a charged rod parallel to a long wire carrying a current. Here’s a step-by-step solution:
Step 1: Understand the Setup
- We have a rod of length l with a uniform charge q distributed along its length.
- The rod is placed parallel to a long straight wire carrying a current i.
- The separation between the rod and the wire is a.
Step 2: Determine the Magnetic Field Due to the Wire
- The magnetic field B at a distance a from a long straight wire carrying current i is given by the formula:
B=μ0I2πa
where μ0 is the permeability of free space.
Step 3: Calculate the Force on the Charged Rod
- The force F on a charge q moving with a velocity v in a magnetic field B is given by:
F=qvBsinθ
where θ is the angle between the velocity vector and the magnetic field vector.
- In this case, since the rod is moving parallel to the magnetic field, θ=90∘ and sin90∘=1. Therefore, we can simplify the equation to:
F=qvB
Step 4: Substitute the Expression for Magnetic Field
- Now we substitute the expression for B from Step 2 into the force equation:
F=qv(μ0I2πa)
Step 5: Final Expression for the Force
- The force required to move the rod with a uniform velocity v is:
F=μ0qIv2πa
Conclusion
- The force needed to move the rod along its length with a uniform velocity v is given by:
F=μ0qIv2πa
- We have a rod of length l with a uniform charge q distributed along its length.
- The rod is placed parallel to a long straight wire carrying a current i.
- The separation between the rod and the wire is a.
- The magnetic field B at a distance a from a long straight wire carrying current i is given by the formula:
B=μ0I2πa
where μ0 is the permeability of free space.
- The force F on a charge q moving with a velocity v in a magnetic field B is given by:
F=qvBsinθ
where θ is the angle between the velocity vector and the magnetic field vector.
- In this case, since the rod is moving parallel to the magnetic field, θ=90∘ and sin90∘=1. Therefore, we can simplify the equation to:
F=qvB
- Now we substitute the expression for B from Step 2 into the force equation:
F=qv(μ0I2πa)
- The force required to move the rod with a uniform velocity v is:
F=μ0qIv2πa
- The force needed to move the rod along its length with a uniform velocity v is given by:
F=μ0qIv2πa
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Comprehension Based
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
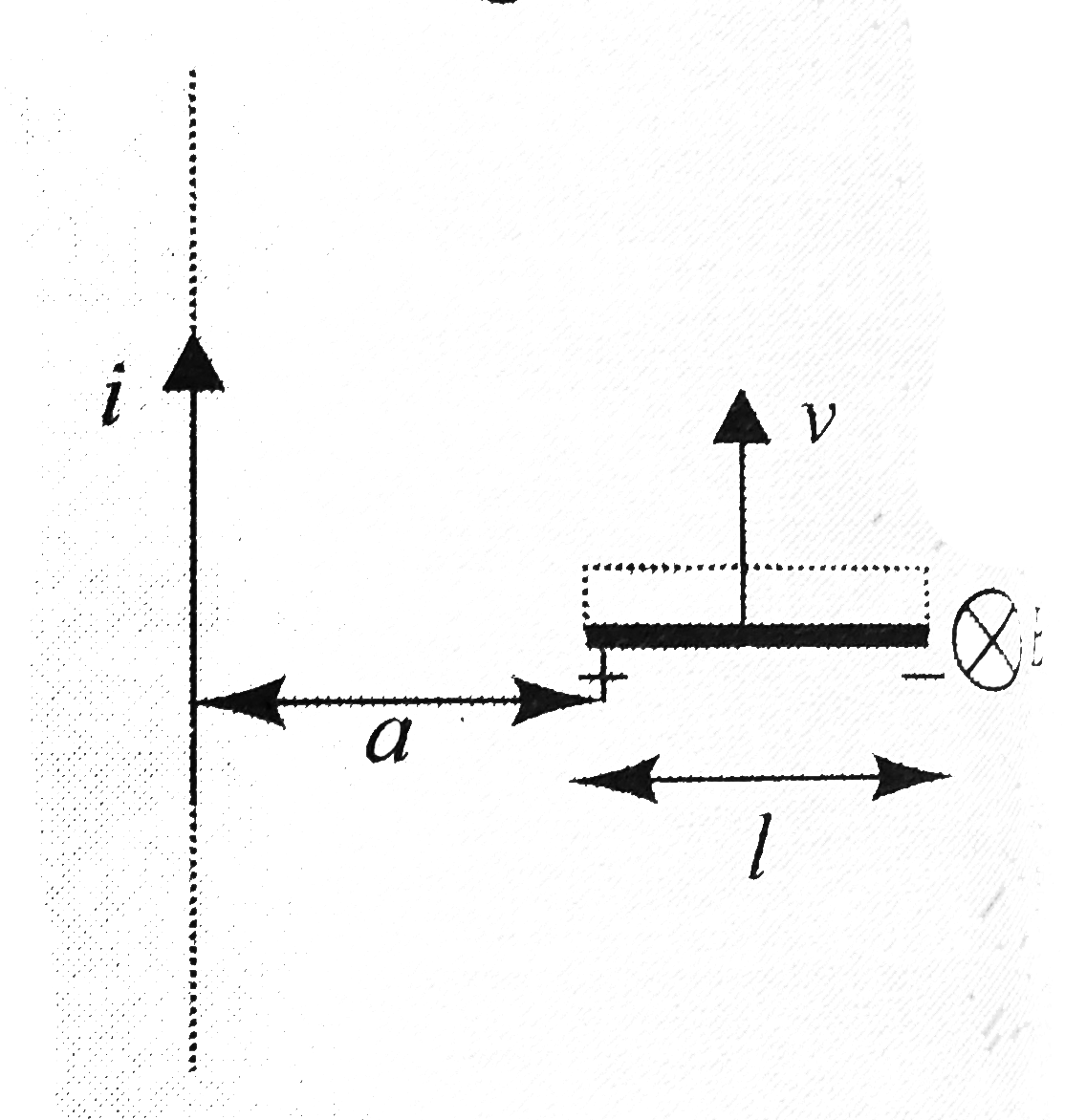
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
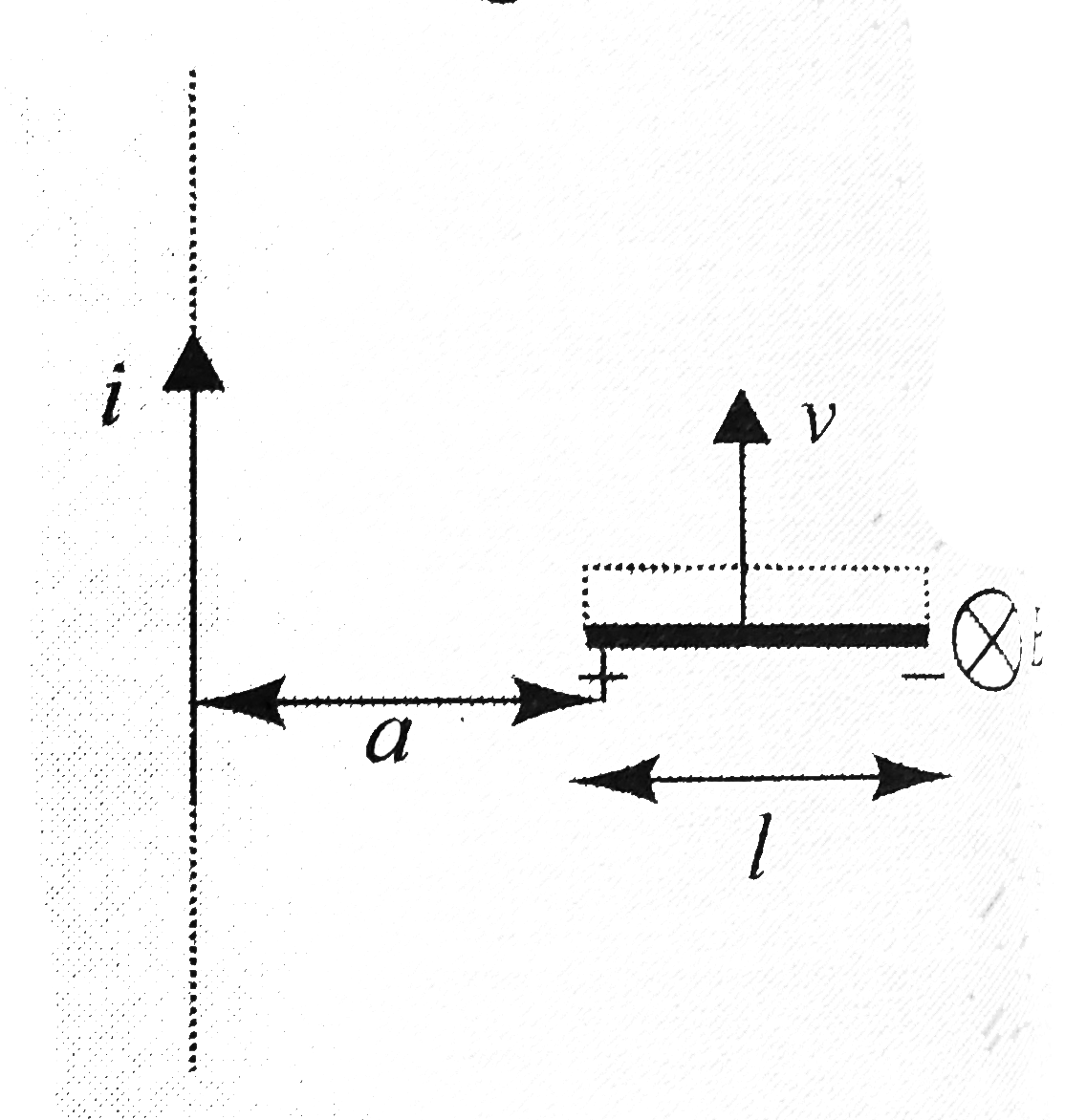
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is x.
View SolutionA thin rod, carrying current i2 is placed near a long straight wire carrying current i1 in the plane of rod as shown in figure. The motion of rod is
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to

View SolutionA rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.
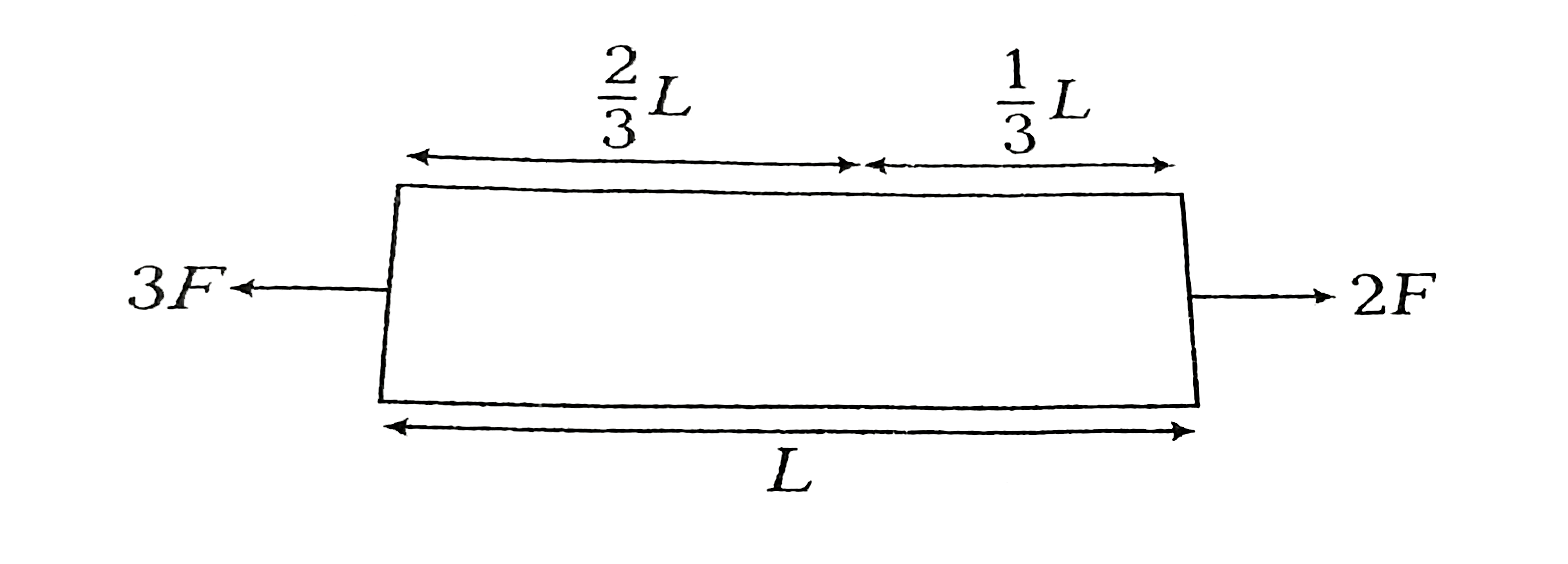
The elongation produced in the rod is
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
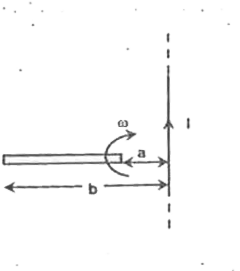
View SolutionA metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
View Solution
