When a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
Tβ
Tln(1β)
Tlnβ
Tlnβ
The correct Answer is:B
To find the time constant of the choke coil when it is short-circuited, we can follow these steps:
Step 1: Understand the Problem
When a choke coil carrying a steady current is short-circuited, the current decreases to a fraction (β) of its initial value (I₀) over a time period (T). We need to find the time constant (τ) of the choke coil.
Step 2: Write the Current Decay Equation
The current in an inductor decays exponentially when the inductor is short-circuited. The equation for the current (I) at time (t) is given by:
I(t)=I0e−t/τ
Where:
- I(t) is the current at time t
- I0 is the initial current
- τ is the time constant
Step 3: Set Up the Equation
According to the problem, at time T, the current decreases to βI0:
βI0=I0e−T/τ
Step 4: Simplify the Equation
We can cancel I0 from both sides (assuming I0≠0):
β=e−T/τ
Step 5: Take the Natural Logarithm
To solve for τ, we take the natural logarithm of both sides:
ln(β)=−Tτ
Step 6: Rearrange to Find the Time Constant
Rearranging the equation gives us:
τ=−Tln(β)
Final Answer
Thus, the time constant τ of the choke coil is:
τ=−Tln(β)
When a choke coil carrying a steady current is short-circuited, the current decreases to a fraction (β) of its initial value (I₀) over a time period (T). We need to find the time constant (τ) of the choke coil.
The current in an inductor decays exponentially when the inductor is short-circuited. The equation for the current (I) at time (t) is given by:
I(t)=I0e−t/τ
Where:
- I(t) is the current at time t
- I0 is the initial current
- τ is the time constant
According to the problem, at time T, the current decreases to βI0:
βI0=I0e−T/τ
We can cancel I0 from both sides (assuming I0≠0):
β=e−T/τ
To solve for τ, we take the natural logarithm of both sides:
ln(β)=−Tτ
Rearranging the equation gives us:
τ=−Tln(β)
Thus, the time constant τ of the choke coil is:
τ=−Tln(β)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Comprehension Based
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
View SolutionConsider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
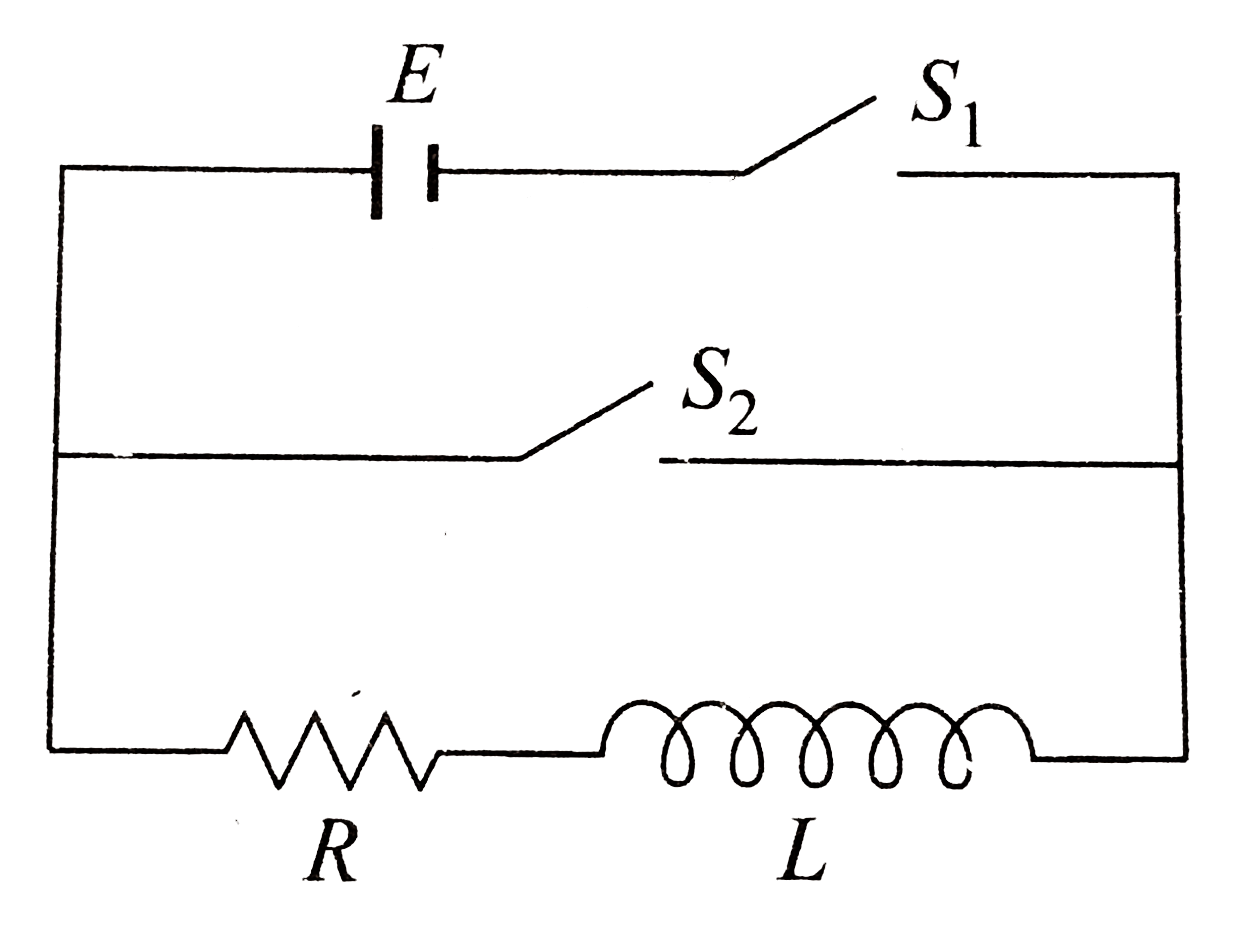
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit is
View SolutionDuring the decay of current in an LR circuit, if the current falls to η times the intial value in time T, then determine the value of time constane.
View SolutionThe current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
View SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View SolutionA choke coil is preferred to a resistance for reducing current in an ac circuit because .
View SolutionHow many time constants will elapse before the current in a charging RC circuit drops to half of its initial value?Answer the same question for a discharging RC circuit.
View SolutionIn an LR circuit, current at t=0 is 20A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
View SolutionHow many time constants will elapse before the current in a charging R−C circuit drops to half of its initial value?
View SolutionFor the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.

View Solution
