During the decay of current in an LR circuit, if the current falls to η times the intial value in time T, then determine the value of time constane.
To determine the value of the time constant τ during the decay of current in an LR circuit, we can follow these steps:
1. Understand the Current Decay Formula:
The current I in an LR circuit decays according to the formula:
I=I0e−tτ
where I0 is the initial current, t is the time, and τ is the time constant.
2. Set Up the Given Condition:
According to the problem, the current falls to η times its initial value after a time T. Therefore, we can express this as:
I=ηI0
and we know that this occurs at time T.
3. Substitute into the Decay Formula:
Substitute I=ηI0 into the decay formula:
ηI0=I0e−Tτ
4. Cancel I0:
Since I0 is common on both sides (assuming I0≠0), we can cancel it:
η=e−Tτ
5. Take the Natural Logarithm:
To solve for τ, take the natural logarithm of both sides:
ln(η)=−Tτ
6. Rearrange to Solve for τ:
Rearranging the equation gives:
τ=−Tln(η)
7. Express in Terms of ln(1/η):
Since ln(η) can be expressed as −ln(1/η), we can rewrite τ as:
τ=Tln(1/η)
Final Answer:
The time constant τ is given by:
τ=Tln(1/η)
---
The current I in an LR circuit decays according to the formula:
I=I0e−tτ
where I0 is the initial current, t is the time, and τ is the time constant.
According to the problem, the current falls to η times its initial value after a time T. Therefore, we can express this as:
I=ηI0
and we know that this occurs at time T.
Substitute I=ηI0 into the decay formula:
ηI0=I0e−Tτ
Since I0 is common on both sides (assuming I0≠0), we can cancel it:
η=e−Tτ
To solve for τ, take the natural logarithm of both sides:
ln(η)=−Tτ
Rearranging the equation gives:
τ=−Tln(η)
Since ln(η) can be expressed as −ln(1/η), we can rewrite τ as:
τ=Tln(1/η)
The time constant τ is given by:
τ=Tln(1/η)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
The value of current I in the circuit will be
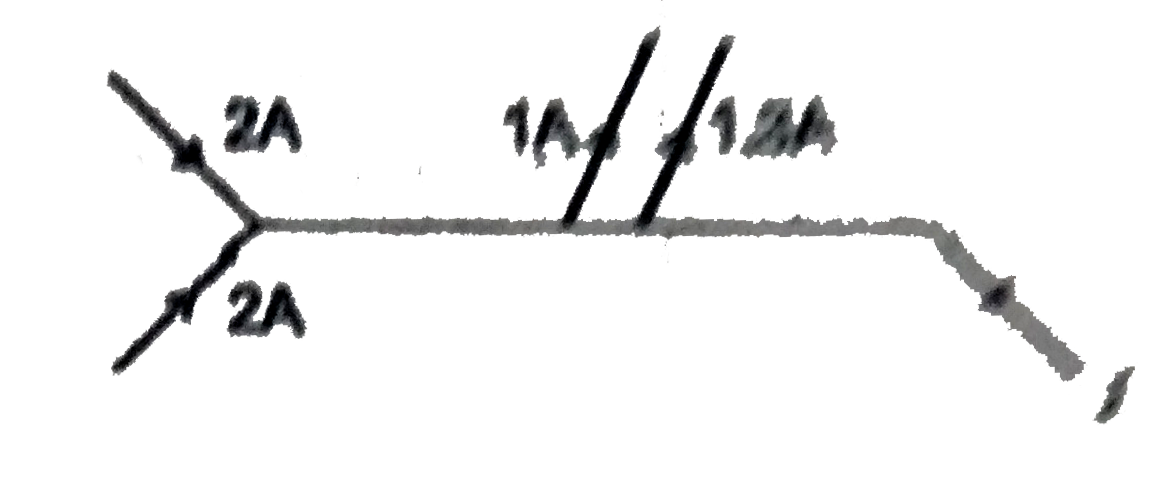
View SolutionWhen a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
View SolutionTime constant of LR circuit will be
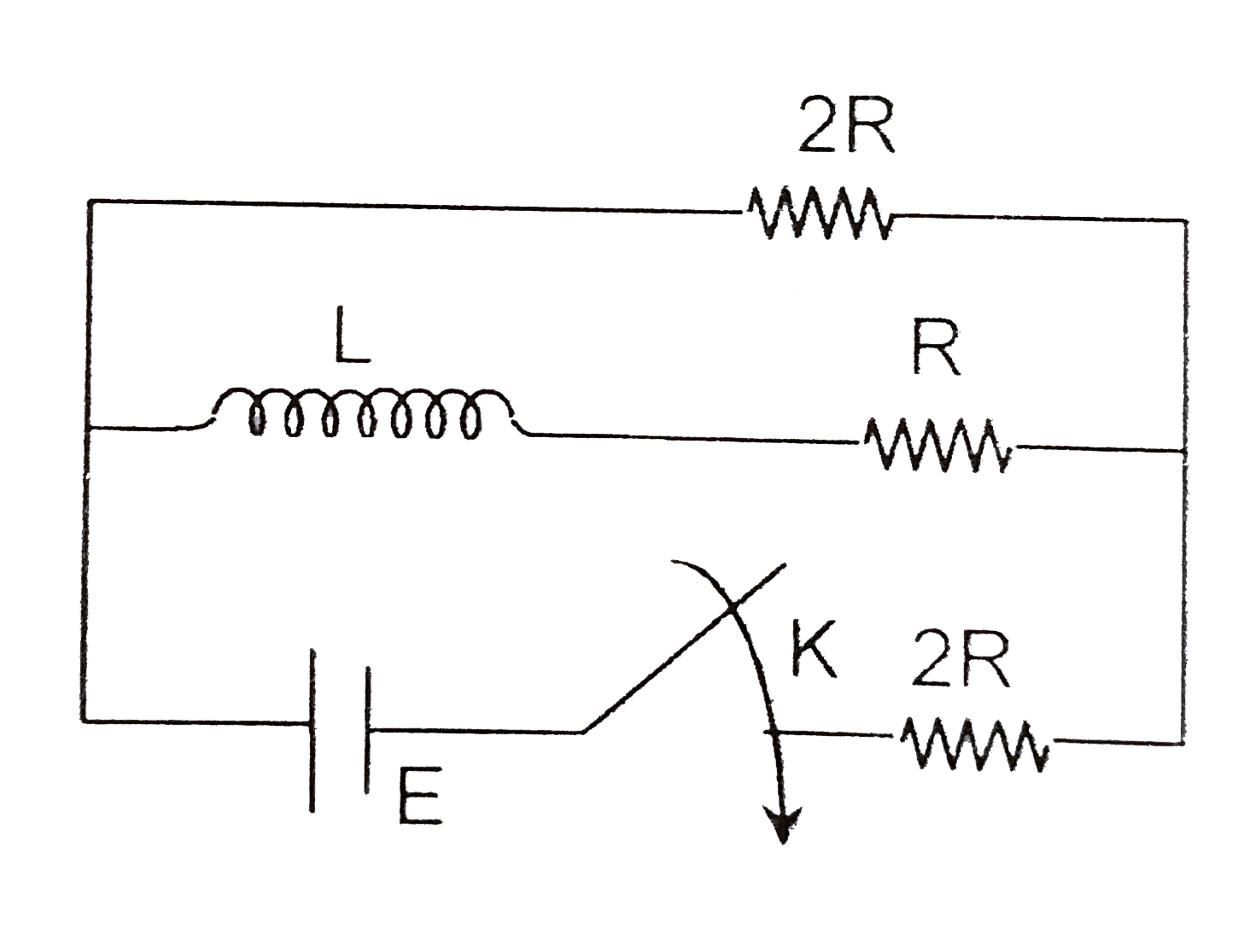
View SolutionIn the given circuit , the value of current is

View Solution
In given LR circuit the switch S is closed at time t=0 then
View SolutionThe current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
View SolutionDuring current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
View SolutionDuring discharging of a capacitor via a resistor
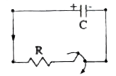
Circuit current varies with time as
View SolutionDuring charging of capacitor in the circuit shown,
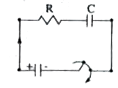
Circuit current versus time graph is
View SolutionIn the given circuit, what is the current I (in A) drawn from battery at time t = 0.
View Solution
