A current i flows along the length of an infinitely long, straight, thin-walled pipe. Then,
(a) the magnetic field at all points inside the pipe is the same, but not zero
(b) the magnetic field at any point inside the pipe is zero
(c) the magnetic field is zero only on the axis of the pipe
(d) the magnetic field is different at different points inside the pipe
To solve the problem of determining the magnetic field inside an infinitely long, straight, thin-walled pipe carrying a current i, we can use Ampere's Circuital Law. Here’s a step-by-step solution:
Step 1: Understand the Configuration
We have an infinitely long, straight, thin-walled pipe with a current i flowing through it. The pipe can be visualized as a hollow cylinder.
Hint: Visualize the pipe as a hollow cylinder with current flowing along its length.
Step 2: Apply Ampere's Circuital Law
Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to μ0 times the total current I enclosed by that loop:
∮B⋅dl=μ0Ienc
Hint: Remember that Ienc is the current enclosed by the loop you choose.
Step 3: Choose an Amperian Loop
To analyze the magnetic field inside the pipe, we can choose a circular Amperian loop of radius r that is entirely inside the pipe (where r is less than the inner radius of the pipe).
Hint: The radius r should be less than the inner radius of the pipe to ensure we are inside it.
Step 4: Determine the Enclosed Current
Inside the thin-walled pipe, the current flows along the surface of the pipe. For any circular loop with a radius r that is less than the inner radius of the pipe, there is no current enclosed by that loop. Thus, Ienc=0.
Hint: Think about how the current is distributed in the pipe and how it affects the enclosed current.
Step 5: Apply Ampere's Law
Since Ienc=0, we substitute this into Ampere's Law:
∮B⋅dl=μ0⋅0=0
This implies that the integral of the magnetic field around the loop is zero.
Hint: A zero integral means that the magnetic field must be uniform and equal to zero throughout the loop.
Step 6: Conclude the Magnetic Field Inside the Pipe
Since the integral of the magnetic field is zero, it follows that the magnetic field B at any point inside the pipe must also be zero:
B=0(inside the pipe)
Hint: Conclude that the magnetic field inside the pipe is zero based on the results from Ampere's Law.
Final Answer
The correct answer is (b) the magnetic field at any point inside the pipe is zero.
---
We have an infinitely long, straight, thin-walled pipe with a current i flowing through it. The pipe can be visualized as a hollow cylinder.
Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to μ0 times the total current I enclosed by that loop:
∮B⋅dl=μ0Ienc
To analyze the magnetic field inside the pipe, we can choose a circular Amperian loop of radius r that is entirely inside the pipe (where r is less than the inner radius of the pipe).
Inside the thin-walled pipe, the current flows along the surface of the pipe. For any circular loop with a radius r that is less than the inner radius of the pipe, there is no current enclosed by that loop. Thus, Ienc=0.
Since Ienc=0, we substitute this into Ampere's Law:
∮B⋅dl=μ0⋅0=0
This implies that the integral of the magnetic field around the loop is zero.
Since the integral of the magnetic field is zero, it follows that the magnetic field B at any point inside the pipe must also be zero:
B=0(inside the pipe)
The correct answer is (b) the magnetic field at any point inside the pipe is zero.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A current I flows along an inflinitely long straight thin walled tube. The magnetic induction at a point inside the tube at a distance r from its wall is
View SolutionA current I ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is .
View SolutionThe magnetic field lines inside a bar magnet
View SolutionFind the magnetic field B at the point P in figure
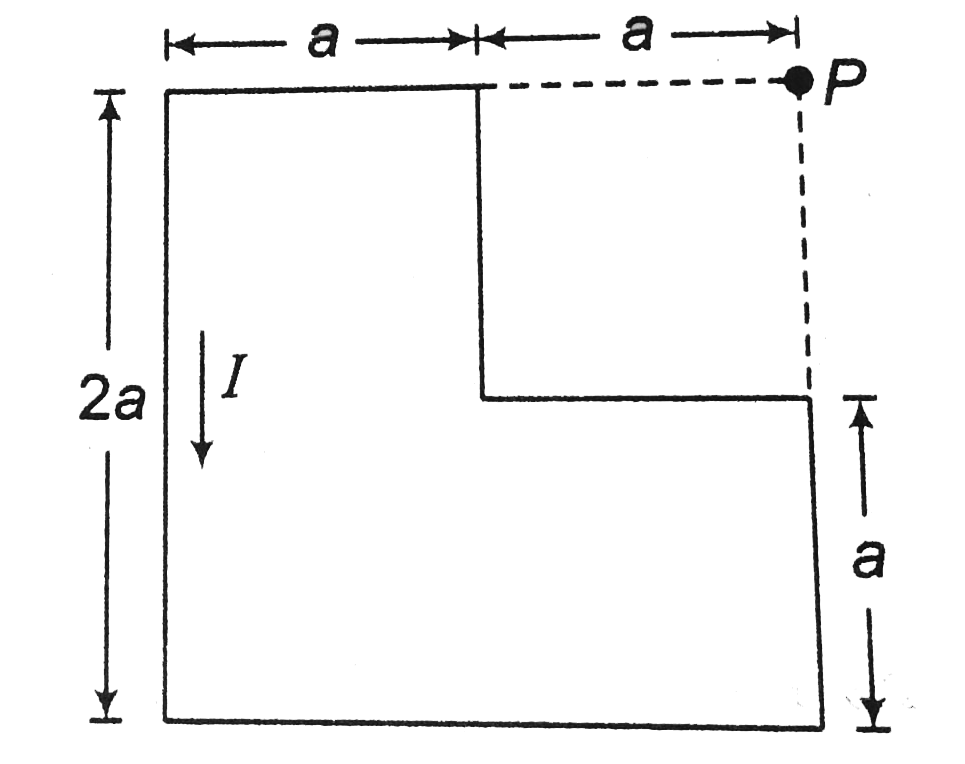 View Solution
View SolutionThe magnetic field inside a solenoid is-
View SolutionFor c=2a if, the magnetic field at point P will be zero when
 View Solution
View SolutionDirection of magnetic field at equatorial point
View SolutionIf an electron enters a magnetic field with its velocity pointing in the same direction as the magnetic field, then
View SolutionThe magnetic field at a point near the centre but outside a current carrying solenoid is zero. Explain why?
View SolutionThe magnetic field at a point x on the axis of a small bar magnet is equal to the field at a point y on the equator of the same magnet. The ratio of the distances of x and y from the centre of the magnet is
View Solution
