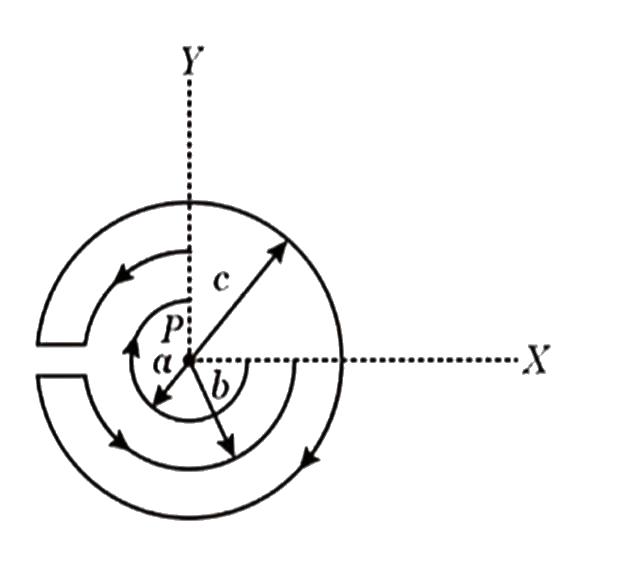
For c=2a if, the magnetic field at point P will be zero when

a=b
a=35b
a=53b
a=13b
The correct Answer is:C
(c) Magnetic field at the centre
B=μ0I2c⊗+μ0I2b(34)⊙+μ0I2a(34)⊗
As per problem:
0=μ0I2[1c−34b+34a]⇒34[1b−1a]=1c
If c=2a,
34[1b−1a]=12a⇒a=53b
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
For c=2aandc<b<c, the magnetic field at the point P will be zero when-
View SolutionWhat is net magnetic field at point O?

View SolutionIn Fig, find the magnetic field at point P.

View SolutionFor adjoining fig, The magnetic field at point, 'P' will be:
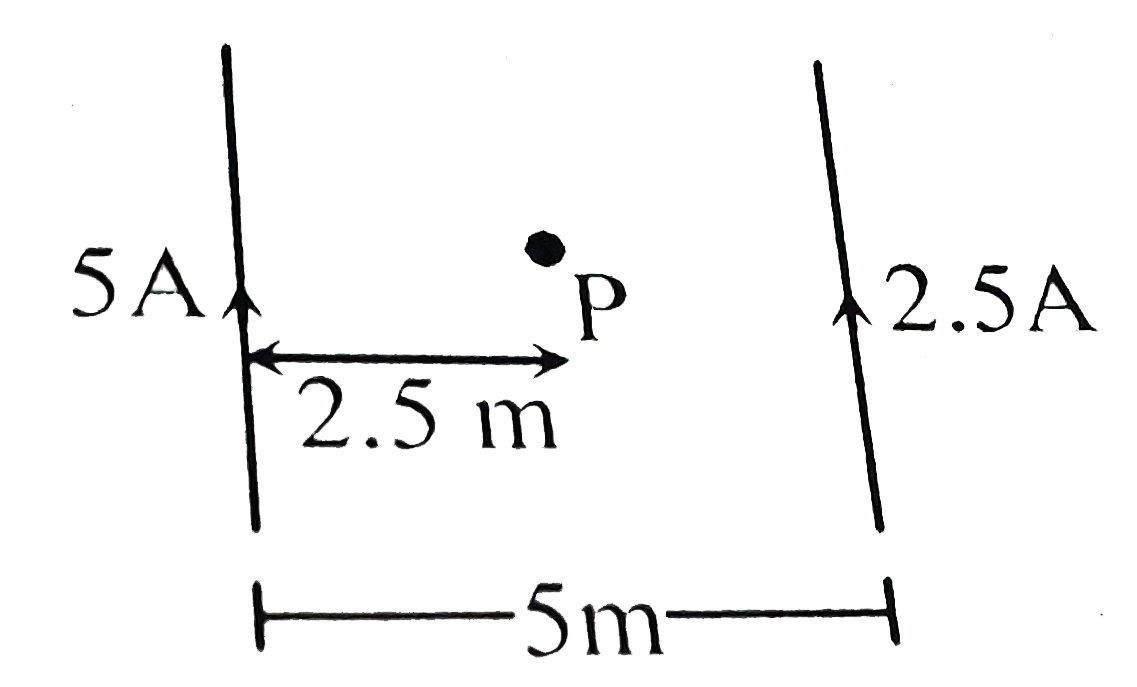
View SolutionFind the magnetic field B at the point P in figure
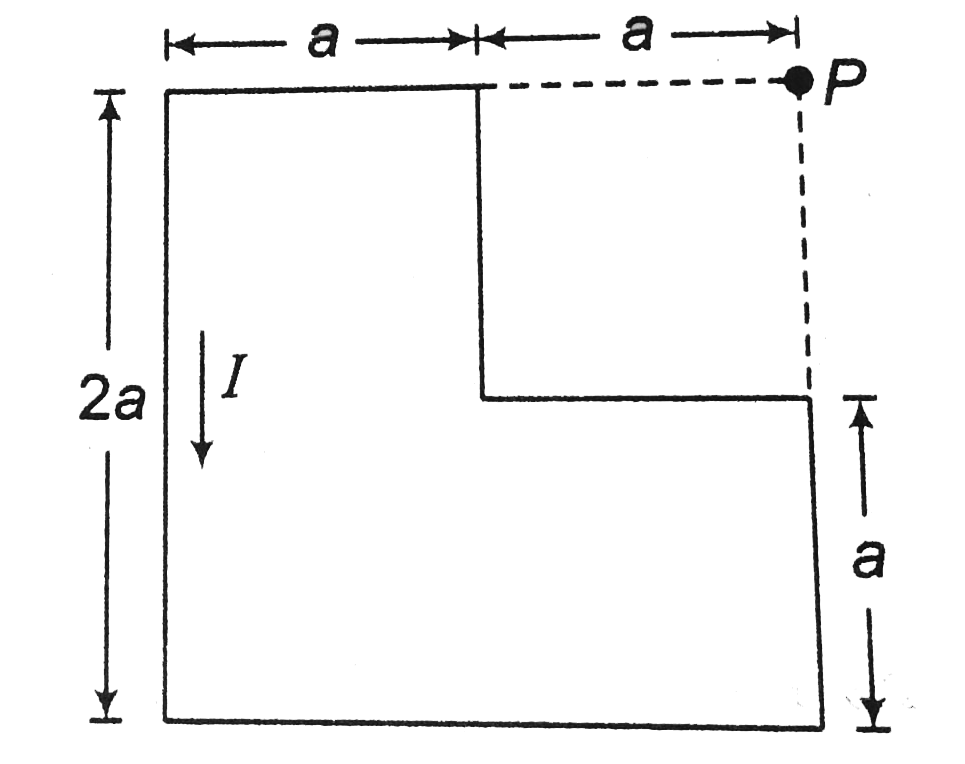
View SolutionFind the magnetic field at point O shown in the figure

View SolutionEach of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances .

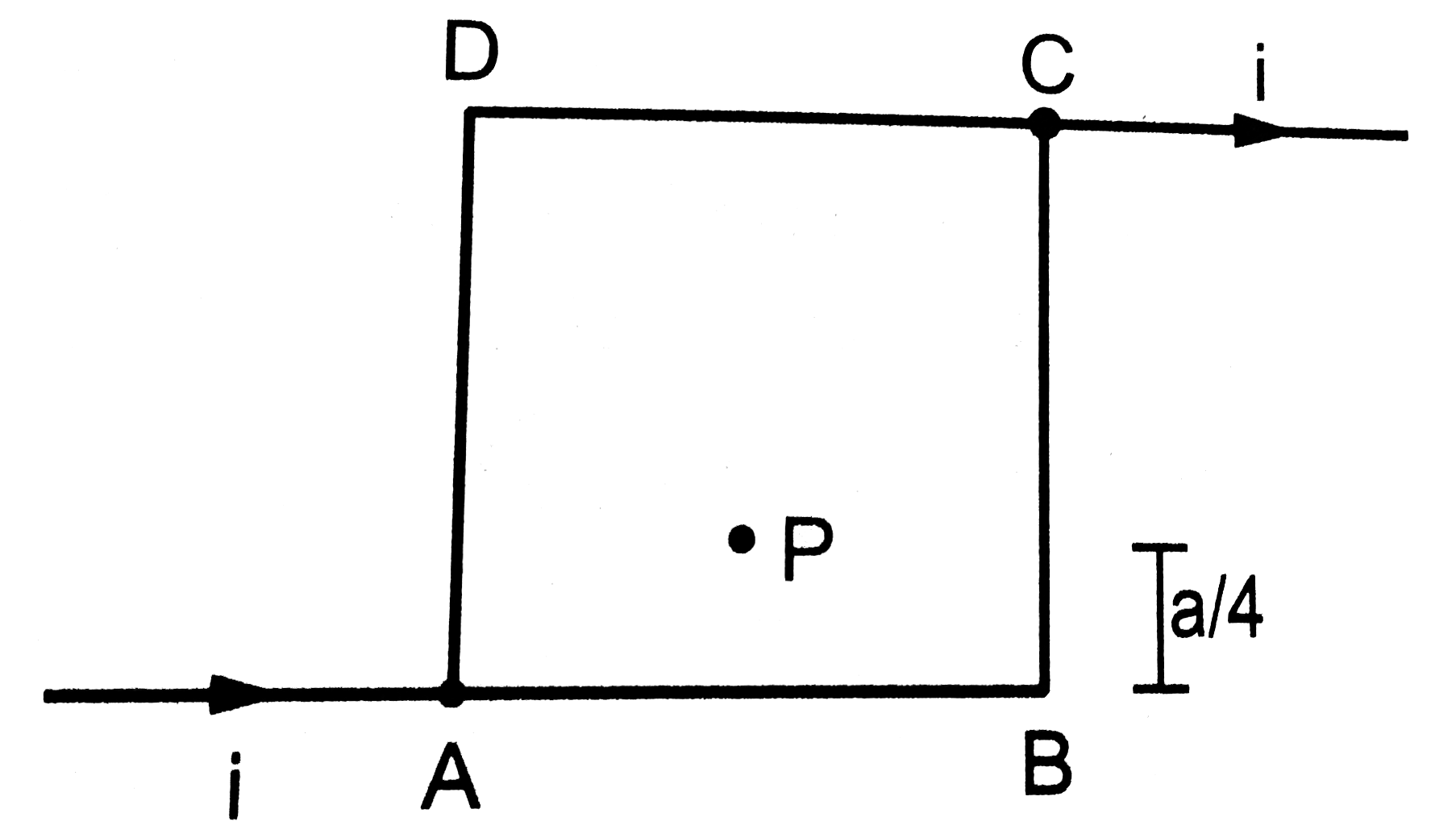
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionIn figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
View Solution