A very long straight conducting wire, lying along the z-axis, carries a current of 2A. The integral ∮→B.d→l is computed along the straight line PQ, where P has the coordinates (2cm,2cm,0) and Q has the coordinates (2cm,2cm,0). The integral has the magnitude (in SI units)
π2×10−7
8π×10−7
2π×10−7
π×10−7
The correct Answer is:A
To solve the problem of calculating the integral ∮→B⋅d→l along the straight line PQ, we can follow these steps:
Step 1: Understand the Setup
We have a long straight conducting wire along the z-axis carrying a current I=2A. The points P and Q are both located at the coordinates (2cm,2cm,0), which means they are the same point. Therefore, the line segment PQ has no length.
Hint: Recognize that if P and Q are the same point, the integral over a closed path will be zero.
Step 2: Calculate the Magnetic Field →B
The magnetic field →B around a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where r is the distance from the wire to the point where we are calculating the magnetic field, and μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Hint: Identify the distance r from the wire to the points P and Q.
Step 3: Determine the Distance r
The coordinates of points P and Q are both (2cm,2cm,0). The distance from the wire (which lies along the z-axis) to the point (2 cm, 2 cm) can be calculated using the Pythagorean theorem:
r=√(2cm)2+(2cm)2=√4+4=√8=2√2cm=0.02√2m
Hint: Convert the distance from centimeters to meters for consistency in SI units.
Step 4: Substitute into the Magnetic Field Formula
Now substituting I=2A and r=0.02√2m into the magnetic field formula:
B=(4π×10−7)⋅22π⋅(0.02√2)
Simplifying this gives:
B=4×10−7⋅20.04√2=8×10−70.04√2=8×10−70.04⋅1.414≈8×10−70.05656≈1.415×10−5T
Hint: Ensure you simplify the fractions correctly.
Step 5: Calculate ∮→B⋅d→l
Since the integral is computed along a path where P and Q are the same point, the length of the path d→l is zero. Therefore:
∮→B⋅d→l=0
Hint: Remember that the integral of a vector field over a path of zero length is zero.
Final Answer
The magnitude of the integral ∮→B⋅d→l is:
0
We have a long straight conducting wire along the z-axis carrying a current I=2A. The points P and Q are both located at the coordinates (2cm,2cm,0), which means they are the same point. Therefore, the line segment PQ has no length.
The magnetic field →B around a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where r is the distance from the wire to the point where we are calculating the magnetic field, and μ0 is the permeability of free space, approximately 4π×10−7T m/A.
The coordinates of points P and Q are both (2cm,2cm,0). The distance from the wire (which lies along the z-axis) to the point (2 cm, 2 cm) can be calculated using the Pythagorean theorem:
r=√(2cm)2+(2cm)2=√4+4=√8=2√2cm=0.02√2m
Now substituting I=2A and r=0.02√2m into the magnetic field formula:
B=(4π×10−7)⋅22π⋅(0.02√2)
Simplifying this gives:
B=4×10−7⋅20.04√2=8×10−70.04√2=8×10−70.04⋅1.414≈8×10−70.05656≈1.415×10−5T
Since the integral is computed along a path where P and Q are the same point, the length of the path d→l is zero. Therefore:
∮→B⋅d→l=0
The magnitude of the integral ∮→B⋅d→l is:
0
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A very long straight conducting wire, lying along the z-axis, carries a current of 2A. The integral ∮→B.d→l is computed along the straight line PQ, where P has the coordinates (2cm,0,0) and Q has the coordinates (2cm,2cm,0). The integral has the magnitude (in SI units)
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
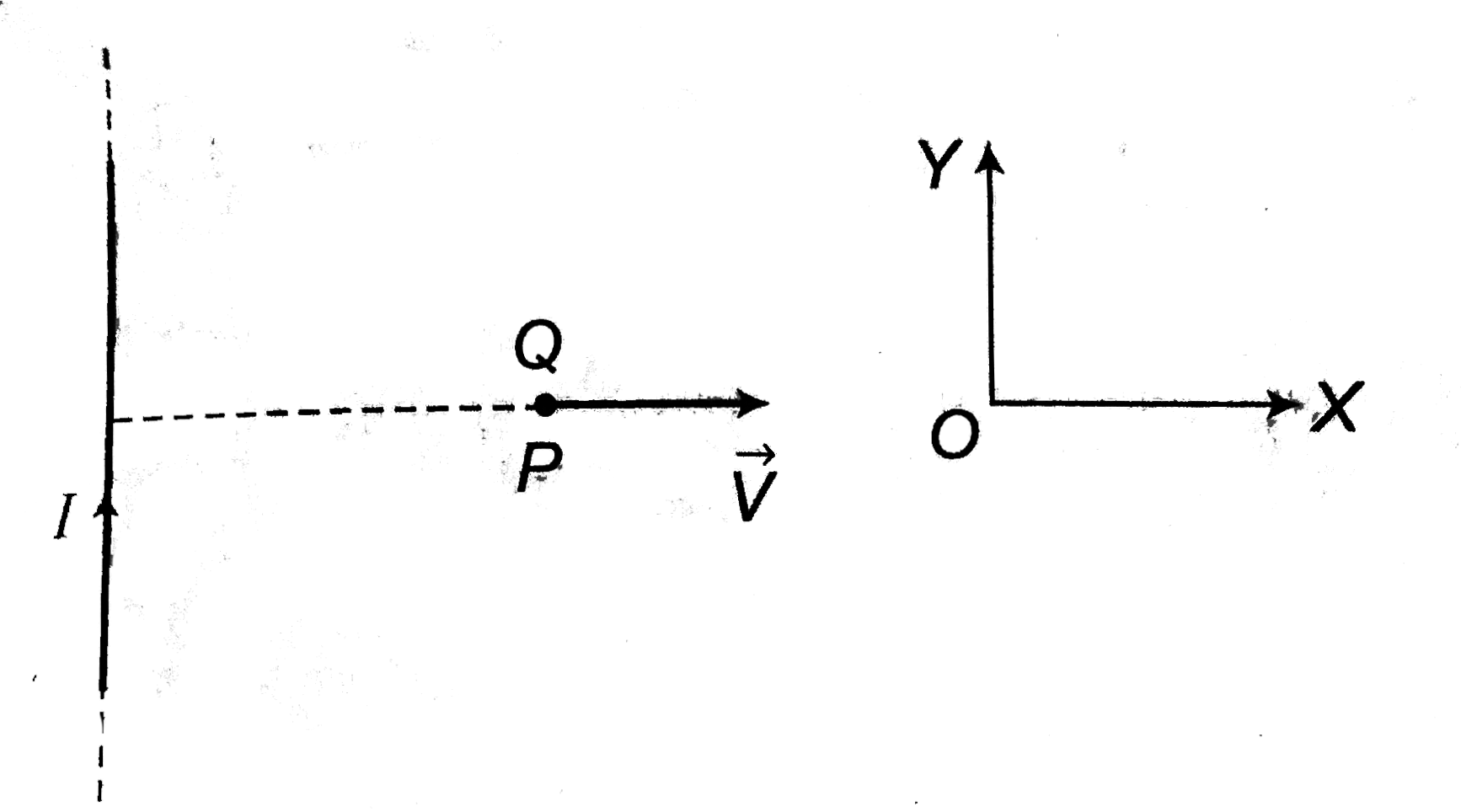
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity→V, as shown, the force on the charge is-
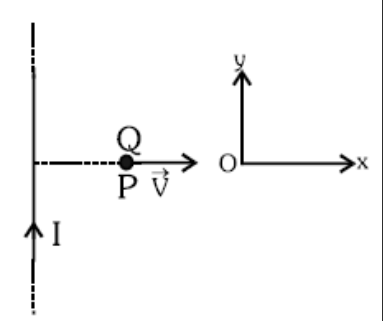
View Solutiona very long straight wire carries a current I. at the instant when are charge -Q at point P has velocity v as shown in figure the force on the charge is

View SolutionFind a unit vector in the direction of −−→PQ, where P and Q have coordinates (5, 0, 8) and (3, 3, 2) respectively.
View SolutionPoint A lies on the curve y=ex2 and has the coordinate (x,e−x2) where x>0. Point B has the coordinates (x,0). If 'O' is the origin, then the maximum area of the ΔAOB is
View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
View SolutionFind the area of the triangle formed by the straight lines y=2x,x=0 and y=2 by integration.
View Solution
