A sphere of charges of radius R carries a positive charge whose volume charge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), whereρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of the electric field as a functiion of the distance r outside the balll is given by
E=ρ0R38εr2
E=ρ0R312εr2
E=ρ0R28εr3
E=ρ0R212εr3
The correct Answer is:B
To find the magnitude of the electric field outside a uniformly charged sphere with a given volume charge density, we can follow these steps:
Step 1: Understand the Charge Density
The charge density is given by:
ρ(r)=ρ0(1−rR)
This means that the charge density varies with the distance r from the center of the sphere.
Step 2: Determine the Total Charge Enclosed
To find the total charge Q enclosed within the sphere, we need to integrate the charge density over the volume of the sphere. The differential charge dq in a thin spherical shell of radius r and thickness dr is given by:
dq=ρ(r)⋅dV=ρ(r)⋅4πr2dr
Substituting the expression for ρ(r):
dq=ρ0(1−rR)⋅4πr2dr
Step 3: Integrate to Find Total Charge
Now we integrate dq from r=0 to r=R:
Q=∫R0dq=∫R0ρ0(1−rR)⋅4πr2dr
This can be simplified as:
Q=4πρ0∫R0(r2−r3R)dr
Calculating the integral:
∫R0r2dr=R33,∫R0r3dr=R44
Substituting these results back:
Q=4πρ0(R33−R44R)=4πρ0(R33−R34)
Combining the fractions:
Q=4πρ0R3(412−312)=4πρ0R3⋅112=4πρ0R312
Step 4: Calculate the Electric Field Outside the Sphere
For points outside the sphere (at a distance r>R), we can use Gauss's law:
E⋅4πr2=Qϵ0
Substituting for Q:
E⋅4πr2=4πρ0R312ϵ0
Solving for E:
E=ρ0R312ϵ0r2
Final Answer
The magnitude of the electric field as a function of the distance r outside the sphere is:
E(r)=ρ0R312ϵ0r2
The charge density is given by:
ρ(r)=ρ0(1−rR)
This means that the charge density varies with the distance r from the center of the sphere.
To find the total charge Q enclosed within the sphere, we need to integrate the charge density over the volume of the sphere. The differential charge dq in a thin spherical shell of radius r and thickness dr is given by:
dq=ρ(r)⋅dV=ρ(r)⋅4πr2dr
Substituting the expression for ρ(r):
dq=ρ0(1−rR)⋅4πr2dr
Now we integrate dq from r=0 to r=R:
Q=∫R0dq=∫R0ρ0(1−rR)⋅4πr2dr
This can be simplified as:
Q=4πρ0∫R0(r2−r3R)dr
Calculating the integral:
∫R0r2dr=R33,∫R0r3dr=R44
Substituting these results back:
Q=4πρ0(R33−R44R)=4πρ0(R33−R34)
Combining the fractions:
Q=4πρ0R3(412−312)=4πρ0R3⋅112=4πρ0R312
For points outside the sphere (at a distance r>R), we can use Gauss's law:
E⋅4πr2=Qϵ0
Substituting for Q:
E⋅4πr2=4πρ0R312ϵ0
Solving for E:
E=ρ0R312ϵ0r2
The magnitude of the electric field as a function of the distance r outside the sphere is:
E(r)=ρ0R312ϵ0r2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of electric field as a function of the distance r inside the sphere is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity is
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The value of distance rm at which electric field intensity is maximum is given by
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
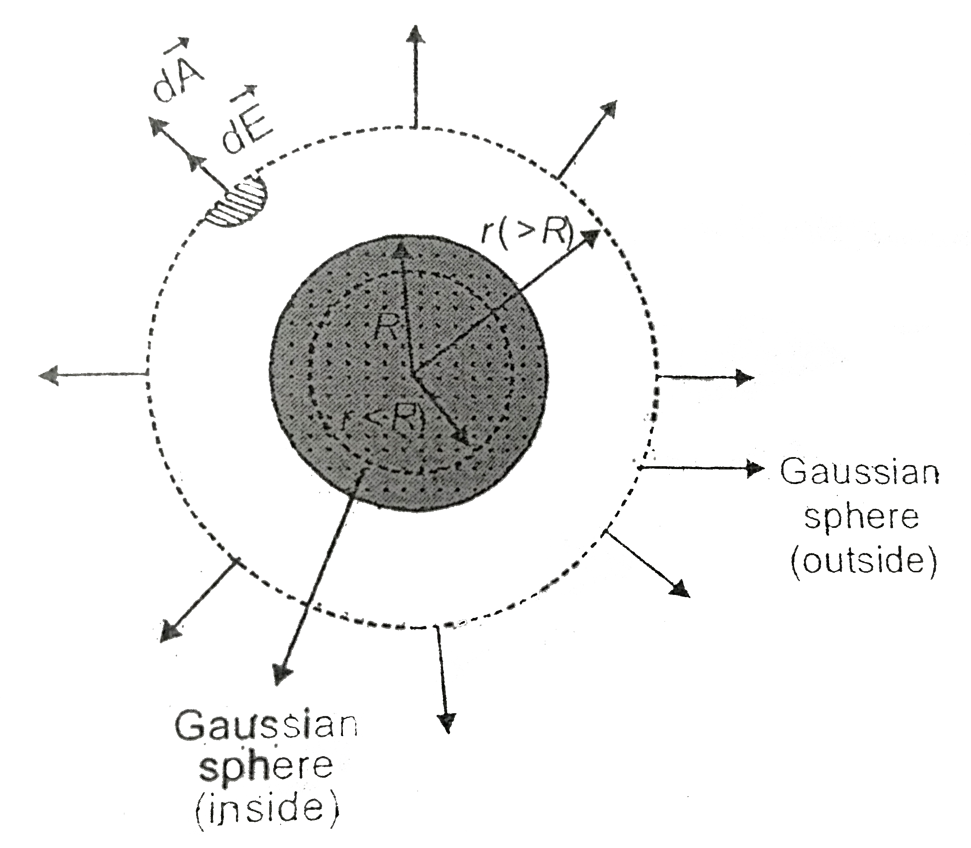
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]

View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionThe curve between charge density ρ and distance r near p−N junction will be
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View Solution
