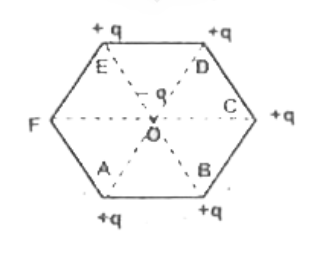
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
14πε0qa2
q16πε0a2
√2q4πε0a2
5q16πε0a2
The correct Answer is:B
To find the magnitude of the net electric field at the center of a regular hexagon with five point charges of +q at its vertices, we can follow these steps:
Step 1: Understand the Configuration
We have a regular hexagon with vertices labeled A, B, C, D, E, and F. Charges of +q are placed at vertices A, B, C, D, and E. Vertex F is empty. The side length of the hexagon is 2a.
Step 2: Determine the Distance from the Center to the Vertices
The distance from the center of the hexagon (point C) to any vertex (A, B, D, or E) can be calculated using the formula for the circumradius \( R \) of a regular hexagon:
\(
R = \frac{s}{\sqrt{3}} = \frac{2a}{\sqrt{3}} = \frac{2a\sqrt{3}}{3}
\)
Step 3: Calculate the Electric Field Due to Each Charge
The electric field \( E \) due to a single point charge \( +q \) at a distance \( r \) is given by:
\(
E = \frac{k \cdot q}{r^2}
\)
where \( k = \frac{1}{4\pi\epsilon_0} \).
Substituting \( r = \frac{2a\sqrt{3}}{3} \):
\(
E = \frac{k \cdot q}{\left(\frac{2a\sqrt{3}}{3}\right)^2} = \frac{k \cdot q}{\frac{4a^2 \cdot 3}{9}} = \frac{9kq}{12a^2} = \frac{3kq}{4a^2}
\)
Step 4: Determine the Direction of Each Electric Field
The electric fields due to the charges at vertices A, B, C, D, and E will have specific directions:
- The electric fields from charges at A, B, D, and E will point away from the respective charges towards the center of the hexagon.
- The charge at vertex F is missing, which means the electric field due to the missing charge would have pointed towards it.
Step 5: Calculate the Net Electric Field
The electric fields from the four charges (A, B, D, and E) will add vectorially. Due to symmetry, the horizontal components of the electric fields from charges at A and D will cancel out, as will the components from B and E.
The vertical components will add up. The resultant electric field \( E_{net} \) at the center due to the four charges can be calculated as:
\(
E_{net} = 4 \cdot E \cdot \sin(60^\circ) = 4 \cdot \frac{3kq}{4a^2} \cdot \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}kq}{a^2}
\)
Final Result
Thus, the magnitude of the net electric field at the center of the hexagon is:
\(
E_{net} = \frac{3\sqrt{3}kq}{a^2}
\)
We have a regular hexagon with vertices labeled A, B, C, D, E, and F. Charges of +q are placed at vertices A, B, C, D, and E. Vertex F is empty. The side length of the hexagon is 2a.
The distance from the center of the hexagon (point C) to any vertex (A, B, D, or E) can be calculated using the formula for the circumradius \( R \) of a regular hexagon:
\(
R = \frac{s}{\sqrt{3}} = \frac{2a}{\sqrt{3}} = \frac{2a\sqrt{3}}{3}
\)
The electric field \( E \) due to a single point charge \( +q \) at a distance \( r \) is given by:
\(
E = \frac{k \cdot q}{r^2}
\)
where \( k = \frac{1}{4\pi\epsilon_0} \).
\(
E = \frac{k \cdot q}{\left(\frac{2a\sqrt{3}}{3}\right)^2} = \frac{k \cdot q}{\frac{4a^2 \cdot 3}{9}} = \frac{9kq}{12a^2} = \frac{3kq}{4a^2}
\)
The electric fields due to the charges at vertices A, B, C, D, and E will have specific directions:
- The electric fields from charges at A, B, D, and E will point away from the respective charges towards the center of the hexagon.
- The charge at vertex F is missing, which means the electric field due to the missing charge would have pointed towards it.
The electric fields from the four charges (A, B, D, and E) will add vectorially. Due to symmetry, the horizontal components of the electric fields from charges at A and D will cancel out, as will the components from B and E.
\(
E_{net} = 4 \cdot E \cdot \sin(60^\circ) = 4 \cdot \frac{3kq}{4a^2} \cdot \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}kq}{a^2}
\)
Thus, the magnitude of the net electric field at the center of the hexagon is:
\(
E_{net} = \frac{3\sqrt{3}kq}{a^2}
\)
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Subjective
Explore 15 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:SUBJECTIVE_TYPE
Explore 6 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Assertion And Reason
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
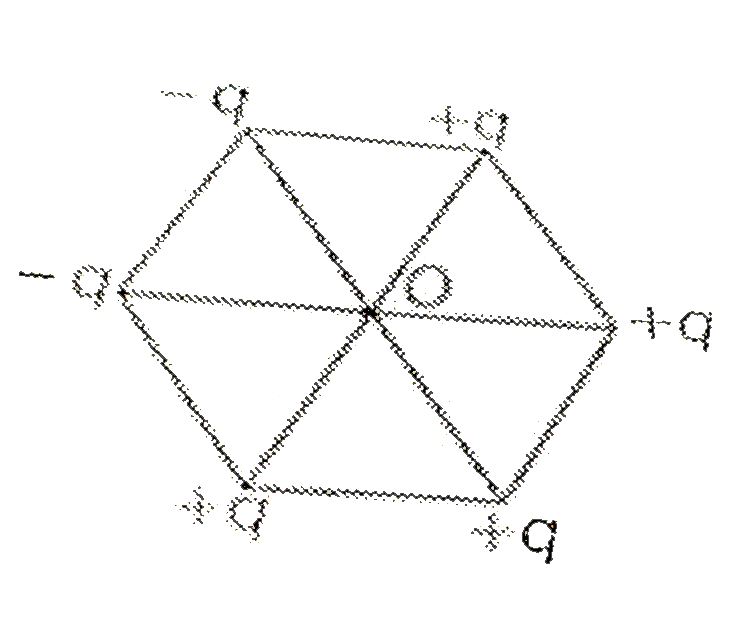
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Five charges, q each are placed at the coreners of a regular pentagone of side.

(a) (i) What will be the electric field at O, the centre of the pentagon ?
(ii) What will be the electric field 0 if the charge from one of the corners (say A) is removed ?
(iii) What will be the electric field at 0 if the charge q at A is replaced by −q ?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its coreners ?
View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionFive point charges, each of value +q coulomb, are placed on five vertices of a regular hexagon of side L meters. The magnitude of the force on the point charge of value -q coulomb, placed at the centre of the hexagon is…………….
View SolutionFive point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….

View SolutionSix point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
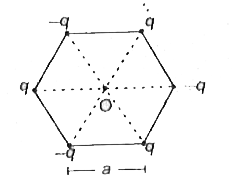
View Solution