A wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
To find the magnetic field at the center of a regular hexagon with a side length of 2 cm carrying a current of 2 A, we can follow these steps:
Step 1: Understand the Configuration
A regular hexagon consists of 6 equal sides. Each side can be treated as a straight wire carrying current. The magnetic field at the center due to each side can be calculated using the formula for the magnetic field due to a finite straight wire.
Step 2: Magnetic Field Due to a Finite Wire
The magnetic field B at a point due to a finite straight wire carrying current I is given by:
B=μ0I4πr(sinα+sinβ)
where:
- μ0 is the permeability of free space (4π×10−7T⋅m/A),
- r is the distance from the wire to the point where the magnetic field is being calculated,
- α and β are the angles subtended by the wire at the point.
Step 3: Determine the Geometry
For a regular hexagon:
- Each internal angle is 120∘.
- The angles α and β for each side at the center will be 30∘ each (since the total angle is 60∘ and is split equally).
Step 4: Calculate the Distance r
The distance r from the center of the hexagon to the midpoint of one of its sides can be calculated as:
r=acos(30∘)
where a=2cm=0.02m. Thus,
r=0.02cos(30∘)=0.02×√32=0.02×0.866=0.01732m
Step 5: Calculate the Magnetic Field for One Side
Now substituting the values into the magnetic field formula for one side:
B=μ0I4πr(sin30∘+sin30∘)=μ0I4πr(0.5+0.5)=μ0I4πr
Substituting I=2A and r=0.01732m:
B=(4π×10−7)×24π×0.01732
This simplifies to:
B=2×10−70.01732=1.1547×10−5T
Step 6: Total Magnetic Field at the Center
Since there are 6 sides contributing equally to the magnetic field at the center, the total magnetic field Btotal is:
Btotal=6×B=6×1.1547×10−5=6.9282×10−5T
Final Answer
The magnetic field at the center of the hexagon is approximately:
Btotal≈6.93×10−5T
A regular hexagon consists of 6 equal sides. Each side can be treated as a straight wire carrying current. The magnetic field at the center due to each side can be calculated using the formula for the magnetic field due to a finite straight wire.
The magnetic field B at a point due to a finite straight wire carrying current I is given by:
B=μ0I4πr(sinα+sinβ)
where:
- μ0 is the permeability of free space (4π×10−7T⋅m/A),
- r is the distance from the wire to the point where the magnetic field is being calculated,
- α and β are the angles subtended by the wire at the point.
For a regular hexagon:
- Each internal angle is 120∘.
- The angles α and β for each side at the center will be 30∘ each (since the total angle is 60∘ and is split equally).
The distance r from the center of the hexagon to the midpoint of one of its sides can be calculated as:
r=acos(30∘)
where a=2cm=0.02m. Thus,
r=0.02cos(30∘)=0.02×√32=0.02×0.866=0.01732m
Now substituting the values into the magnetic field formula for one side:
B=μ0I4πr(sin30∘+sin30∘)=μ0I4πr(0.5+0.5)=μ0I4πr
Substituting I=2A and r=0.01732m:
B=(4π×10−7)×24π×0.01732
This simplifies to:
B=2×10−70.01732=1.1547×10−5T
Since there are 6 sides contributing equally to the magnetic field at the center, the total magnetic field Btotal is:
Btotal=6×B=6×1.1547×10−5=6.9282×10−5T
The magnetic field at the center of the hexagon is approximately:
Btotal≈6.93×10−5T
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEY ENGLISHChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
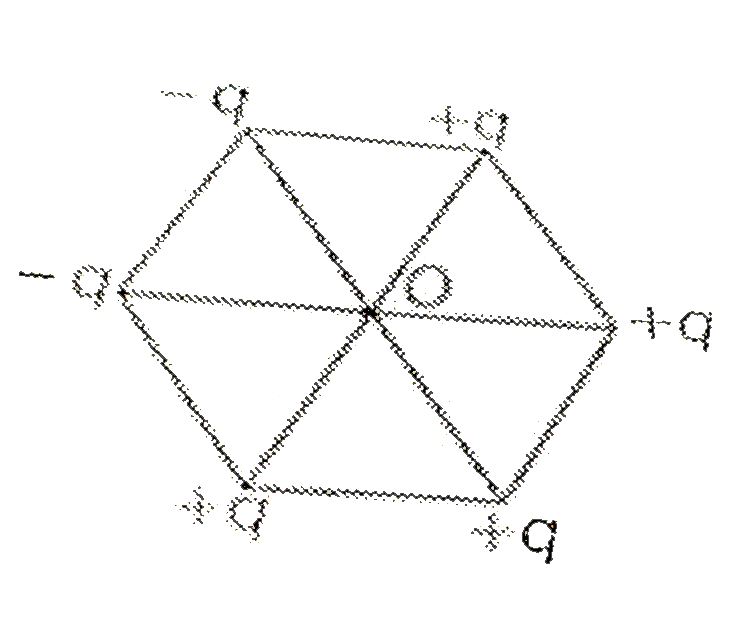
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83qA hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104V
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionSix point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
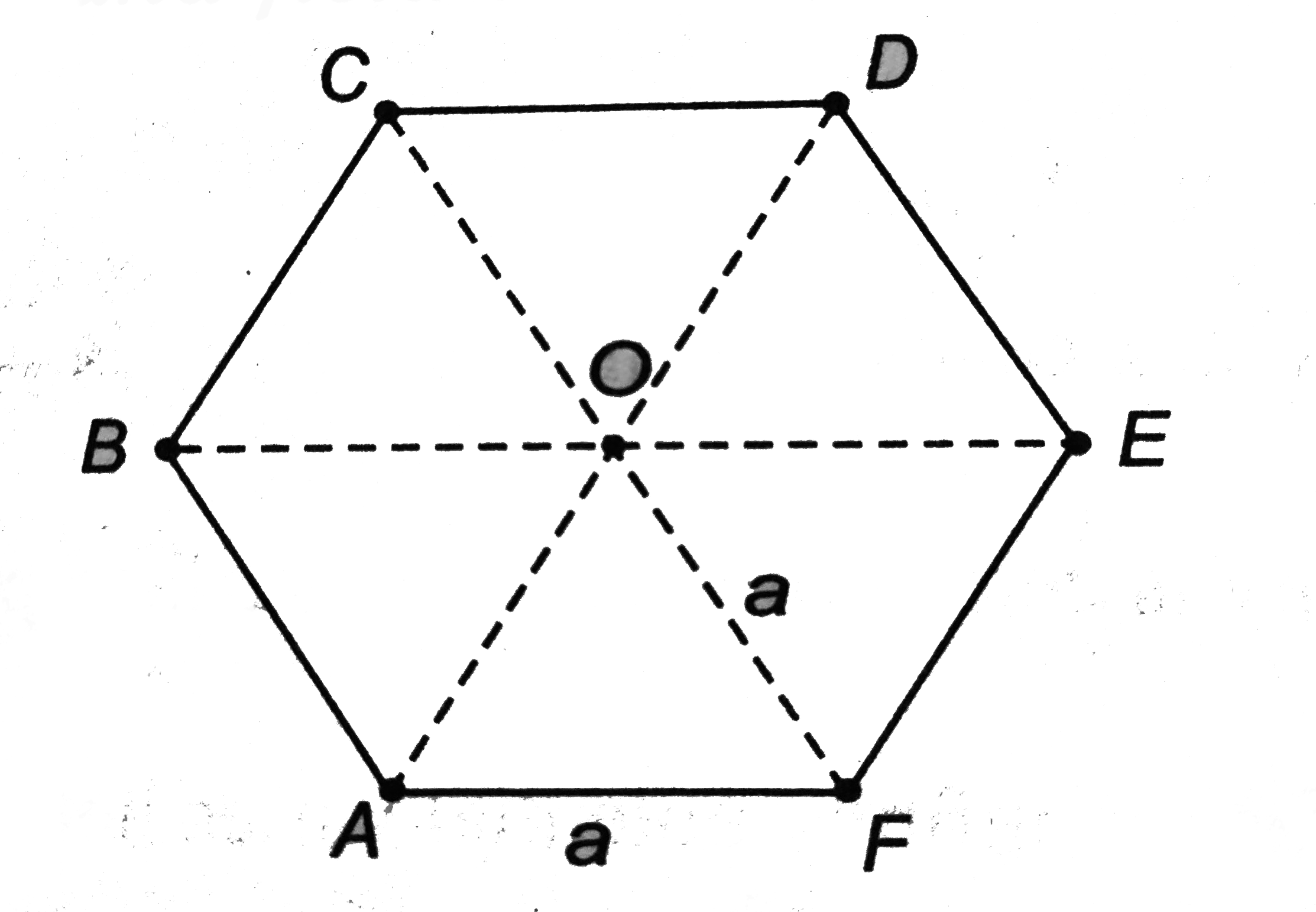 .
.
View Solution

