Two point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
the electric field E at all point on the axis has the same direction.
E at all points on the y-axis is along ˆi
positive work is done in bringing a test charge from infinity to the origin
All of the above
The correct Answer is:B
To solve the problem, we need to analyze the electric field created by two point charges, +q and -q, located at (-a, 0) and (a, 0) respectively.
1. Understanding the Setup:
- We have two charges: +q at point (-a, 0) and -q at point (a, 0).
- The x-axis is the line along which the charges are placed, and the y-axis is perpendicular to it.
2. Electric Field Due to Each Charge:
- The electric field (E) due to a point charge is given by the formula:
E=k|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the field is being calculated.
3. Electric Field at the Origin (0, 0):
- At the origin, the electric field due to +q is directed away from the charge (to the right) and the electric field due to -q is directed towards the charge (to the left).
- Since both charges are equidistant from the origin, the magnitudes of the electric fields due to both charges at the origin are equal, but they are in opposite directions. Thus, they cancel each other out:
Enet=E+q+E−q=0
4. Electric Field Along the x-axis:
- If we move along the x-axis (to the left or right of the origin), the electric field due to the positive charge (+q) will always point away from it (to the right), while the electric field due to the negative charge (-q) will always point towards it (to the left).
- As we move away from the origin towards the left, the influence of the positive charge decreases, and the influence of the negative charge increases. Thus, the net electric field will point to the left.
- Conversely, as we move to the right, the influence of the negative charge decreases, and the influence of the positive charge increases, making the net electric field point to the right.
5. Electric Field Along the y-axis:
- On the y-axis, the electric fields due to both charges will have components that cancel each other out. The y-components of the electric fields from both charges will be equal in magnitude but opposite in direction, thus resulting in a net electric field that is directed along the x-axis (i.e., along the i-cap direction).
6. Potential at the Origin:
- The electric potential (V) at the origin due to both charges can be calculated as:
V=k+qa+k−qa=0
- Since the potential at infinity is also 0, the work done in bringing a test charge from infinity to the origin is:
W=QΔV=Q(0−0)=0
7. Conclusion:
- The electric field at all points on the x-axis does not have the same direction.
- The electric field at all points on the y-axis is directed along the i-cap direction.
- The work done in bringing a test charge from infinity to the origin is zero.
Final Answer:
The correct option is B: The electric field at all points on the y-axis is along the i-cap direction.
- We have two charges: +q at point (-a, 0) and -q at point (a, 0).
- The x-axis is the line along which the charges are placed, and the y-axis is perpendicular to it.
- The electric field (E) due to a point charge is given by the formula:
E=k|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the field is being calculated.
- At the origin, the electric field due to +q is directed away from the charge (to the right) and the electric field due to -q is directed towards the charge (to the left).
- Since both charges are equidistant from the origin, the magnitudes of the electric fields due to both charges at the origin are equal, but they are in opposite directions. Thus, they cancel each other out:
Enet=E+q+E−q=0
- If we move along the x-axis (to the left or right of the origin), the electric field due to the positive charge (+q) will always point away from it (to the right), while the electric field due to the negative charge (-q) will always point towards it (to the left).
- As we move away from the origin towards the left, the influence of the positive charge decreases, and the influence of the negative charge increases. Thus, the net electric field will point to the left.
- Conversely, as we move to the right, the influence of the negative charge decreases, and the influence of the positive charge increases, making the net electric field point to the right.
- On the y-axis, the electric fields due to both charges will have components that cancel each other out. The y-components of the electric fields from both charges will be equal in magnitude but opposite in direction, thus resulting in a net electric field that is directed along the x-axis (i.e., along the i-cap direction).
- The electric potential (V) at the origin due to both charges can be calculated as:
V=k+qa+k−qa=0
- Since the potential at infinity is also 0, the work done in bringing a test charge from infinity to the origin is:
W=QΔV=Q(0−0)=0
- The electric field at all points on the x-axis does not have the same direction.
- The electric field at all points on the y-axis is directed along the i-cap direction.
- The work done in bringing a test charge from infinity to the origin is zero.
The correct option is B: The electric field at all points on the y-axis is along the i-cap direction.
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Subjective
Explore 15 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:SUBJECTIVE_TYPE
Explore 6 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Assertion And Reason
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
Similar Questions
In the figure, two point charges +qand−q are placed on the x-axis at (+a,0)and(−a,0) respectively. A tiny dipole of dipolem moment (p) is kept at the origin along the y-axis. The torque on the dipole equals

View SolutionTwo point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges +8q and -2q are located at x=0 and x=L respectively. The location of a point on the x-axis from +8q at which the net electric field due to these two point charges is zero is
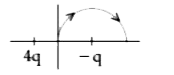
View SolutionA two point charges 4q and -q are fixed on the x - axis x=−d2andx=d2 , respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View Solution

