An infinite line of charge λ per unit length is placed along the y-axis. The work done in moving a charge q from A(a,0) to B(2a,0) is
qλ2πε0"ln" 2
qλ2πε0ln(12)
qλ4πε0)ln√2
qλ4πε0ln2
The correct Answer is:B
To solve the problem of finding the work done in moving a charge q from point A(a,0) to point B(2a,0) in the electric field created by an infinite line charge with linear charge density λ, we can follow these steps:
Step 1: Understand the Electric Field due to an Infinite Line Charge
The electric field E at a distance x from an infinite line charge with linear charge density λ is given by the formula:
E=2kλx
where k=14πϵ0.
Step 2: Set Up the Work Done Formula
The work done W in moving a charge q from point A to point B can be expressed as:
W=q(VB−VA)
where VB and VA are the electric potentials at points B and A respectively.
Step 3: Relate Work Done to Electric Field
The work done can also be expressed in terms of the electric field:
W=−q∫BAE⋅dx
Since the movement is along the x-axis, we can simplify this to:
W=−q∫2aaEdx
Step 4: Substitute the Electric Field into the Integral
Substituting the expression for E:
W=−q∫2aa2kλxdx
Step 5: Solve the Integral
We can factor out the constants:
W=−q⋅2kλ∫2aa1xdx
The integral of 1x is lnx:
W=−q⋅2kλ(lnx)2aa
Calculating the definite integral gives:
W=−q⋅2kλ(ln(2a)−ln(a))
This simplifies to:
W=−q⋅2kλln(2aa)=−q⋅2kλln(2)
Step 6: Substitute k Back
Substituting k=14πϵ0:
W=−q⋅2⋅14πϵ0⋅λln(2)
This simplifies to:
W=−qλ2πϵ0ln(2)
Final Result
Thus, the work done in moving the charge q from point A to point B is:
W=−qλ2πϵ0ln(2)
The electric field E at a distance x from an infinite line charge with linear charge density λ is given by the formula:
E=2kλx
where k=14πϵ0.
The work done W in moving a charge q from point A to point B can be expressed as:
W=q(VB−VA)
where VB and VA are the electric potentials at points B and A respectively.
The work done can also be expressed in terms of the electric field:
W=−q∫BAE⋅dx
Since the movement is along the x-axis, we can simplify this to:
W=−q∫2aaEdx
Substituting the expression for E:
W=−q∫2aa2kλxdx
We can factor out the constants:
W=−q⋅2kλ∫2aa1xdx
The integral of 1x is lnx:
W=−q⋅2kλ(lnx)2aa
Calculating the definite integral gives:
W=−q⋅2kλ(ln(2a)−ln(a))
This simplifies to:
W=−q⋅2kλln(2aa)=−q⋅2kλln(2)
Substituting k=14πϵ0:
W=−q⋅2⋅14πϵ0⋅λln(2)
This simplifies to:
W=−qλ2πϵ0ln(2)
Thus, the work done in moving the charge q from point A to point B is:
W=−qλ2πϵ0ln(2)
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Subjective
Explore 15 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:SUBJECTIVE_TYPE
Explore 6 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Level 1 Assertion And Reason
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
Similar Questions
For an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
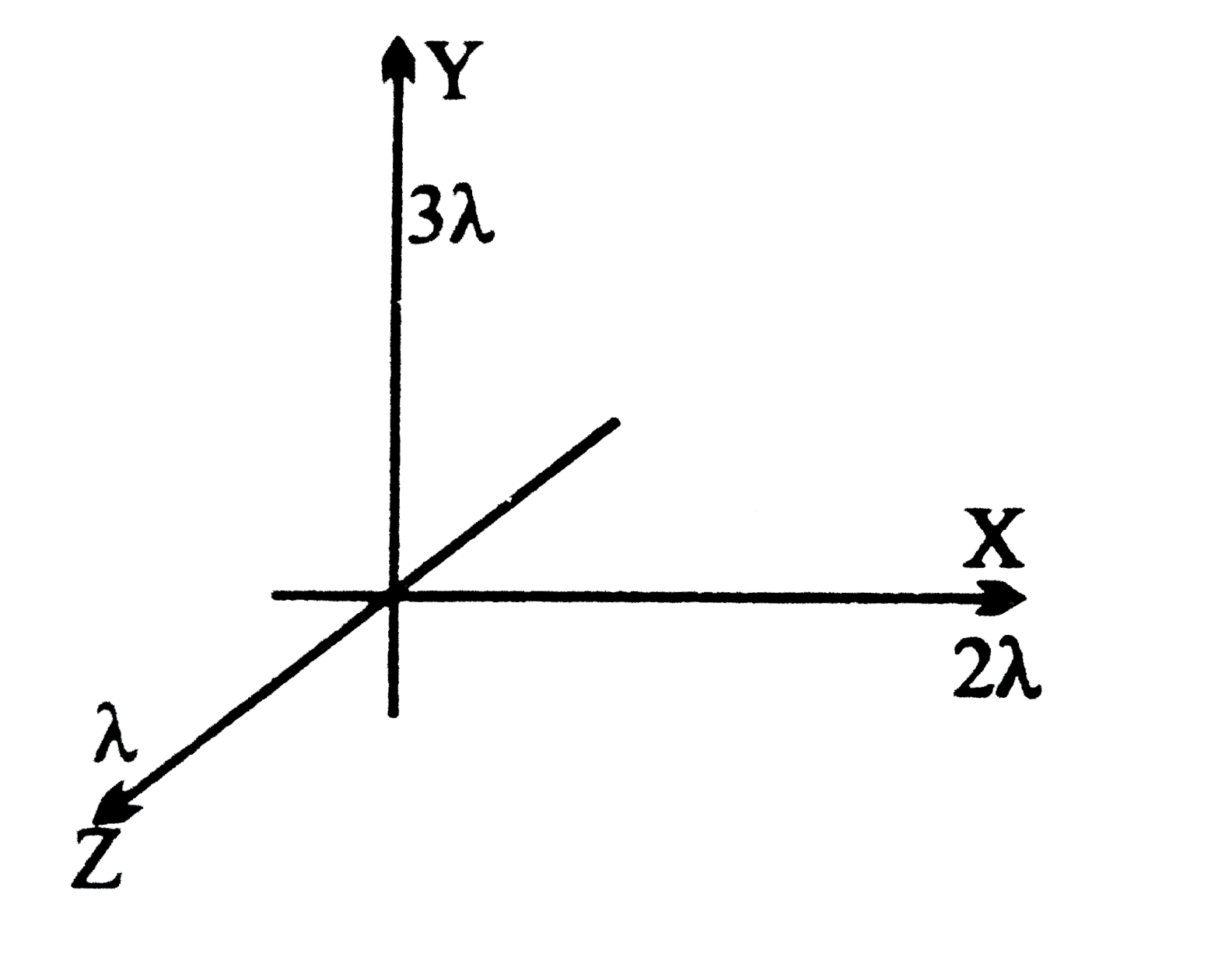
View SolutionThe diagram shows three infinitely long uniform line charges placed on the X,Y and Z axis . The work done in moving a unit positive charge from (1,1,1) to (0 , 1,1,) is equal to
 .
.
View Solution
Knowledge Check
The work done to move a unit charge along an equipotential from P to Q
Amust be defined as −Q∫P→E.→dlBis zeroCcan have a non-zero valueDboth (a) and (b)are correctA charge is distributed with a linear density λ over a rod of the length L placed along radius vector drawn from the point where a point charge q is located. The distance between q and the nearest point on linear charge is R. The electrical force experienced by the linear charge due to q is
AqλL4πε0R2BqλL4πε0R(R+L)CqλL4πε0RLDqλL4πε0L2
The work done to move a charge along an equipotential from A to B
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionA point charge +q is placed at origin O. The work done in taking another point charge -q from the point A to point B along the circular arc as shown in the figure is
_PHY_E05_122_Q01.png) .
.
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

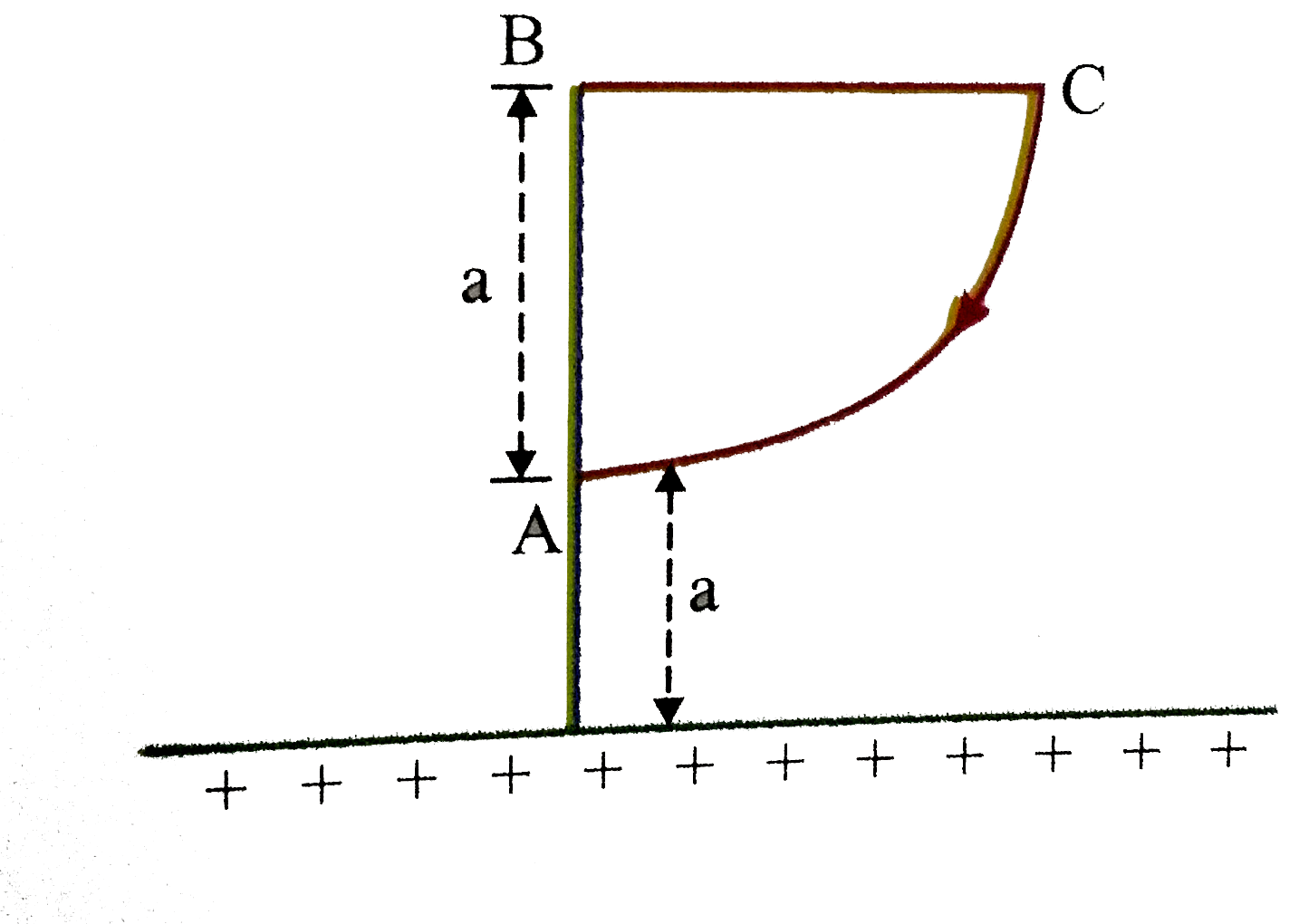
View SolutionThe arc AB with the centre C and the infinitely long wire having linear charge density λ are lying in the same place. The minimum amount of work to be done to move a point charge q0 from point A to B through a circuit path AB of radius a is equal to

View Solution

