What is the charge per unit area in C/m2 of an infinite plane sheet of charge if the electric field produced by the sheet of charge has magnitude 3.0N/C?
The correct Answer is:A, B, C
To find the charge per unit area (σ) of an infinite plane sheet of charge given the electric field (E) produced by the sheet, we can use the formula:
E=σ2ϵ0
where:
- E is the electric field (in N/C),
- σ is the charge per unit area (in C/m²),
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Step 1: Rearranging the Formula
We need to rearrange the formula to solve for σ:
σ=2Eϵ0
Step 2: Substituting the Values
Now we can substitute the given values into the equation. We know:
- E=3.0N/C
- ϵ0=8.85×10−12C2/N m2
Substituting these values into the equation:
σ=2×3.0N/C×8.85×10−12C2/N m2
Step 3: Calculating σ
Now we perform the multiplication:
σ=6.0×8.85×10−12
Calculating this gives:
σ=53.1×10−12C/m2
Step 4: Final Result
Converting this to scientific notation:
σ=5.31×10−11C/m2
Thus, the charge per unit area of the infinite plane sheet of charge is:
σ=5.31×10−11C/m2
---
- E is the electric field (in N/C),
- σ is the charge per unit area (in C/m²),
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
We need to rearrange the formula to solve for σ:
Now we can substitute the given values into the equation. We know:
- E=3.0N/C
- ϵ0=8.85×10−12C2/N m2
Now we perform the multiplication:
Converting this to scientific notation:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
For two infinitely long charged parallel sheets, the electric feild at P will be
View SolutionA ring of charge with radius 0.5m has 0.002π m gap. If the ribg carries a charge of +1C the electric field at the center is

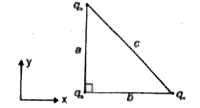
View SolutionSuppose that three point charges qa,qb and qc are arranged at the vertices of a right -angled triangle as shown . What is the absolute electric potential at the position of the third charge if qa=−6.0μC,qb=+4.0μC,qc=+2.0μC,a=4.0m and b=3.0 m ? Suppose that the third charge which is initially at rest is repelled to infinity by the combined electric field of the other two charges which are held fixed . What is the final final kinetic energy of the third charge ?
View SolutionAn injfinite large sheet has charg density σC/m2 Find electric field at a distance d perendicular to the sheet.
View SolutionThe electric field on two sides of a thin sheet of charge is shown in the figure. The charge density on the sheet is
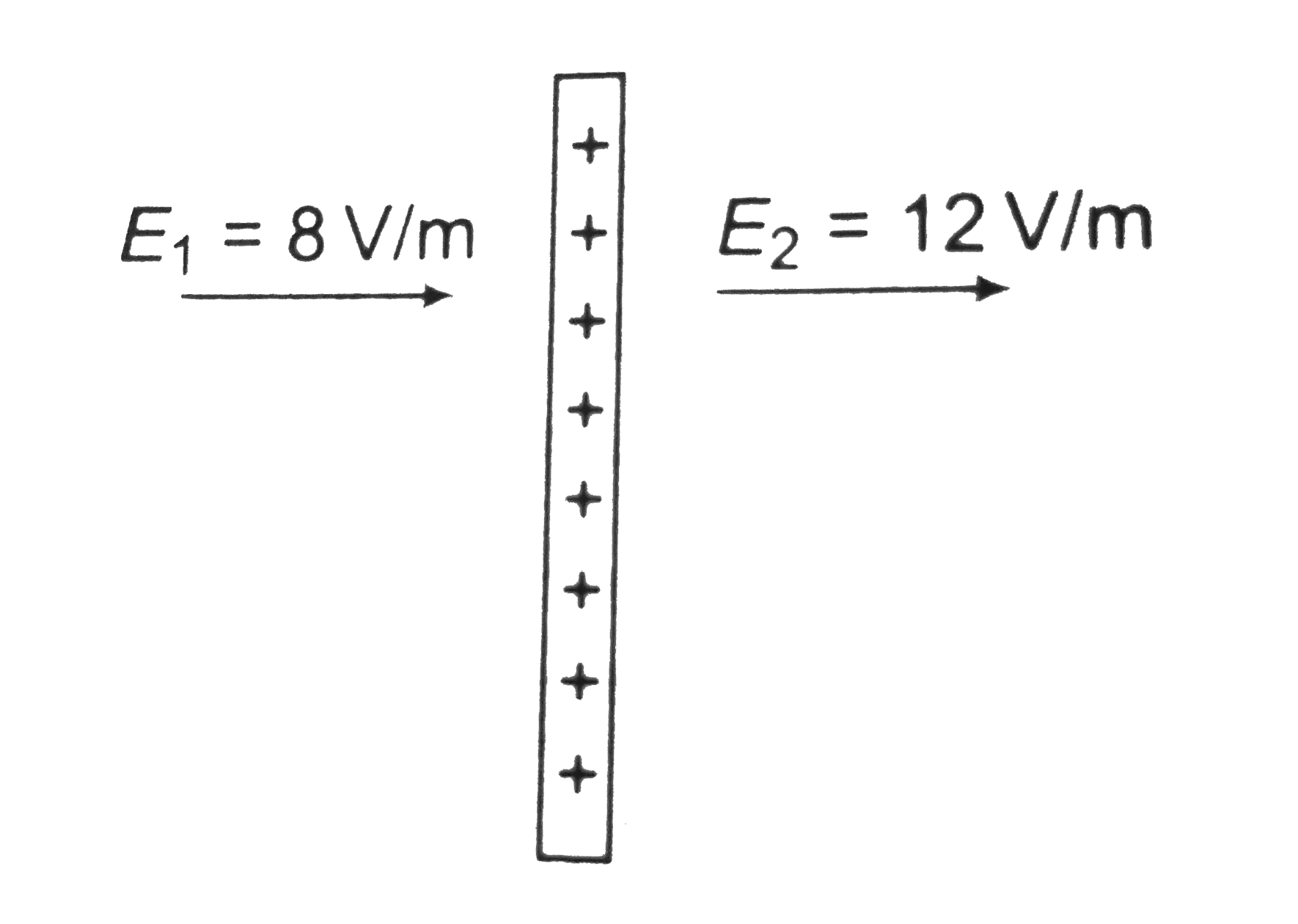
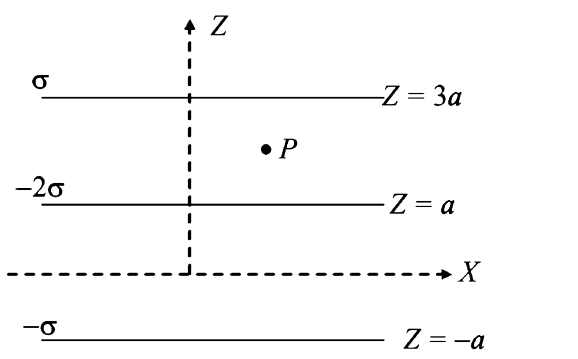
View SolutionThree infinitely long charge sheets are placed as shown in figure. The electric field at point P is
View SolutionAnswer the following:
(i) Use Gauss' law to find the electric field due to a uniformly charged infinite plane sheet. What is the direction of field for positive and negative charge densities?
(ii) Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitance in the ratio 1:2 so that the energy stored in the two cases becomes the same.
View SolutionThe figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area +σ,+2σ and −σ. Find the ratio of the net electric field at that point a to that at point B.
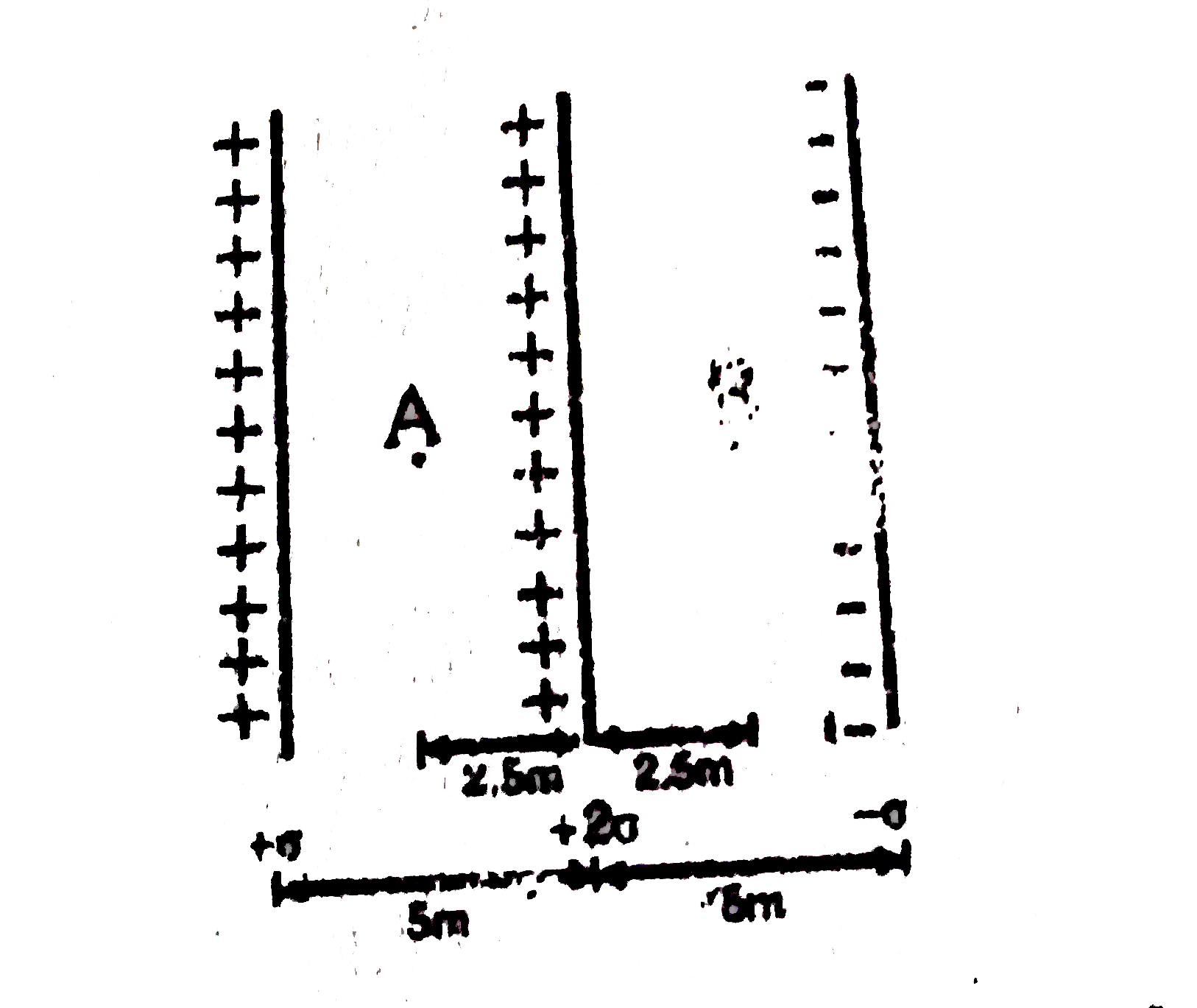
View SolutionA large charged metal sheet is placed in a uniform electric field, perpendicular to the electric field lines. After placing the sheet into the field, the electric field on the left side of the sheet is E1=5×105Vm−1 and on the right it is E2=3×105Vm−1. The sheet experiences a net electric force of 0.08 N. Find the area of one face of the sheet. Assume the external field to remain constant after introducing the large sheet. Use
(14πε0)=9×109Nm2C−2

View SolutionAn isolated conducting sheet of area A and carrying a charge Q is placed in a uniform electric field E, such that the electric field is perpendicular to the sheet and covers all the sheet. Find out the charges appearing on its two surfaces.

View Solution
