A charged particle of mass m=1 kg and charge q=2μC is thrown from a horizontal ground at an angle θ=45∘ with the speed 25m/s. In space, a horizontal electric field E=2×107 V/m exists in the direction of motion. Find the range on horizontal ground of the projectile thrown. Take g=10m/s2.
The correct Answer is:A, B, C
To find the range of the charged particle thrown at an angle of 45 degrees in the presence of an electric field, we will follow these steps:
Step 1: Identify the given values
- Mass of the particle, m=1kg
- Charge of the particle, q=2μC=2×10−6C
- Initial speed, u=25m/s
- Angle of projection, θ=45∘
- Electric field, E=2×107V/m
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the horizontal and vertical components of the initial velocity
The initial velocity can be resolved into horizontal and vertical components using trigonometric functions:
- Horizontal component, ux=ucosθ=25cos45∘=25×1√2=25√2≈17.68m/s
- Vertical component, uy=usinθ=25sin45∘=25×1√2=25√2≈17.68m/s
Step 3: Calculate the horizontal acceleration due to the electric field
The horizontal acceleration ax caused by the electric field can be calculated using the formula:
ax=qEm
Substituting the values:
ax=(2×10−6)×(2×107)1=0.04m/s2
Step 4: Calculate the total time of flight
The total time of flight T can be calculated using the formula:
T=2uyg
Substituting the values:
T=2×17.6810=3.536s
Step 5: Calculate the range
The range R can be calculated using the formula:
R=uxT+12axT2
Substituting the known values:
R=(17.68)(3.536)+12(0.04)(3.536)2
Calculating each term:
1. uxT=17.68×3.536≈62.5m
2. 12axT2=12×0.04×(3.536)2≈0.5×0.04×12.5≈0.25m
Adding these together:
R≈62.5+0.25=62.75m
Final Result
The range of the projectile on the horizontal ground is approximately R≈62.75m.
---
- Mass of the particle, m=1kg
- Charge of the particle, q=2μC=2×10−6C
- Initial speed, u=25m/s
- Angle of projection, θ=45∘
- Electric field, E=2×107V/m
- Acceleration due to gravity, g=10m/s2
The initial velocity can be resolved into horizontal and vertical components using trigonometric functions:
- Horizontal component, ux=ucosθ=25cos45∘=25×1√2=25√2≈17.68m/s
- Vertical component, uy=usinθ=25sin45∘=25×1√2=25√2≈17.68m/s
The horizontal acceleration ax caused by the electric field can be calculated using the formula:
ax=qEm
Substituting the values:
ax=(2×10−6)×(2×107)1=0.04m/s2
The total time of flight T can be calculated using the formula:
T=2uyg
Substituting the values:
T=2×17.6810=3.536s
The range R can be calculated using the formula:
R=uxT+12axT2
Substituting the known values:
R=(17.68)(3.536)+12(0.04)(3.536)2
Calculating each term:
1. uxT=17.68×3.536≈62.5m
2. 12axT2=12×0.04×(3.536)2≈0.5×0.04×12.5≈0.25m
R≈62.5+0.25=62.75m
The range of the projectile on the horizontal ground is approximately R≈62.75m.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A charged particle of mass m=1 kg and charge q=2μC is thrown for a horizotal ground at an angle θ=45∘ with speed 20m/s. In space a horizontal electric field E=2×107 V/m exist. Find the range on horizontal ground of the projectile thrown.
View SolutionA charged particle of mass m = 2 kg and charge 1μC is projected from a horizontal ground at an angle θ=45∘ with speed 10ms−1. In space, a horizontal electric field towards the direction of projection E=2×107NC−1 exists. The range of the projectile is
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
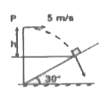
View SolutionA bullet is fired with speed 50m/s at 45∘ angle with horizontal. Find the height of the bullet when its direction of motion makes angle 30∘ with the horizontal.
View SolutionA simple pendulum with a bob of mass m=1 kg, charge q=5μC and string length imis given a horizontal velocity a in a uniform electric field E=2×106Vm at its bottommost point A, as shown in figure. It is given that the speed a is such that the particle leaves the circle at point C. Find the speed a (Take g=10ms2)
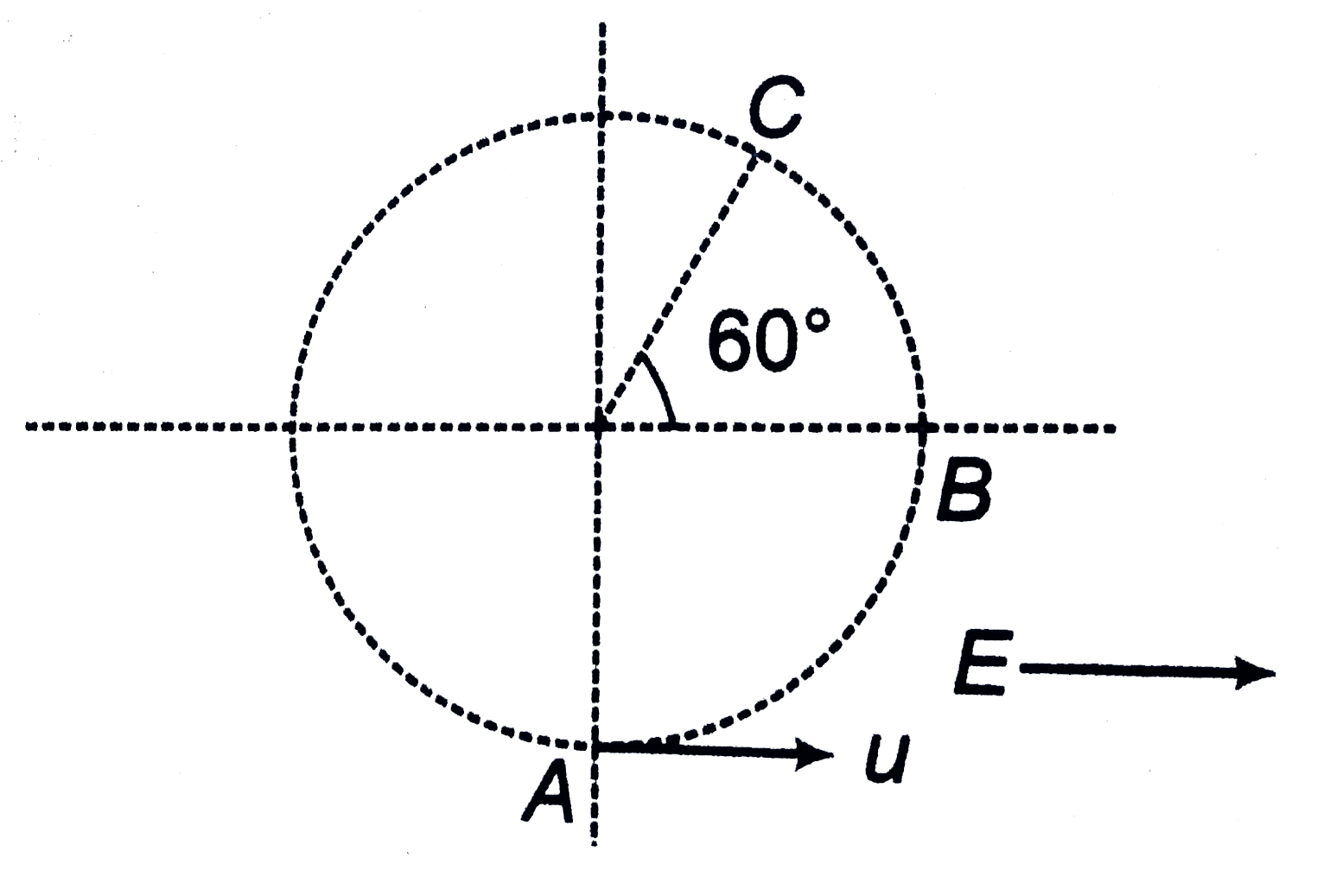
View SolutionAn electric field is acting vertically upwards . A particle of mass 1 mg and charge −1μC is projected with a velocity 20m/s at an angle 45∘ with the horizontal . Its horizontal range is 10 m, then the intensity of electric field is (g=10m/s2)
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View SolutionEquation of trajector of ground to ground projectile is y=2x−9x2. Then the angle of projection with horizontal and speed of projection is : (g=10m/s2)
View SolutionEquation of trajector of ground to ground projectile is y=2x−9x2. Then the angle of projection with horizontal and speed of projection is : (g=10m/s2)
View Solution
