An electric field of exists along the x-axis in space. Calculate the potential difference where the points A and B are given by
a.
b.
The correct Answer is:B, D
To solve the problem of calculating the potential difference VB−VA for the given electric field and points, we will follow these steps:
Part (a): Points A = (0, 0) and B = (4 m, 2 m)
1. Identify the Electric Field:
The electric field E is given as 20N/C along the x-axis. This can be represented as:
E=20^iN/C
2. Set Up the Integral for Potential Difference:
The potential difference VB−VA can be calculated using the formula:
VB−VA=−∫BAE⋅dr
Here, dr is the differential displacement vector.
3. Parameterize the Path:
Since the electric field is only in the x-direction, we can simplify the integral. The displacement vector dr can be expressed as dx^i+dy^j. However, since the electric field does not have a y-component, we will only consider the x-component for the calculation.
4. Determine the Limits of Integration:
The limits for x will be from 0 to 4 (the x-coordinate of point B). The y-coordinate does not affect the potential difference in this case.
5. Evaluate the Integral:
The integral simplifies to:
VB−VA=−∫4020dx=−20(x)40=−20(4−0)=−80V
Part (b): Points A = (4 m, 2 m) and B = (6 m, 5 m)
1. Identify the Electric Field:
The electric field remains the same:
E=20^iN/C
2. Set Up the Integral for Potential Difference:
Again, we use the formula:
VB−VA=−∫BAE⋅dr
3. Parameterize the Path:
For this part, we will consider the x-component of the path from x=4 to x=6. The y-component does not contribute to the potential difference.
4. Determine the Limits of Integration:
The limits for x will be from 4 to 6.
5. Evaluate the Integral:
The integral becomes:
VB−VA=−∫6420dx=−20(x)64=−20(6−4)=−40V
Final Answers:
- For part (a): VB−VA=−80V
- For part (b): VB−VA=−40V
The electric field E is given as 20N/C along the x-axis. This can be represented as:
E=20^iN/C
The potential difference VB−VA can be calculated using the formula:
VB−VA=−∫BAE⋅dr
Here, dr is the differential displacement vector.
Since the electric field is only in the x-direction, we can simplify the integral. The displacement vector dr can be expressed as dx^i+dy^j. However, since the electric field does not have a y-component, we will only consider the x-component for the calculation.
The limits for x will be from 0 to 4 (the x-coordinate of point B). The y-coordinate does not affect the potential difference in this case.
The integral simplifies to:
VB−VA=−∫4020dx=−20(x)40=−20(4−0)=−80V
The electric field remains the same:
E=20^iN/C
Again, we use the formula:
VB−VA=−∫BAE⋅dr
For this part, we will consider the x-component of the path from x=4 to x=6. The y-component does not contribute to the potential difference.
The limits for x will be from 4 to 6.
The integral becomes:
VB−VA=−∫6420dx=−20(x)64=−20(6−4)=−40V
- For part (a): VB−VA=−80V
- For part (b): VB−VA=−40V
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
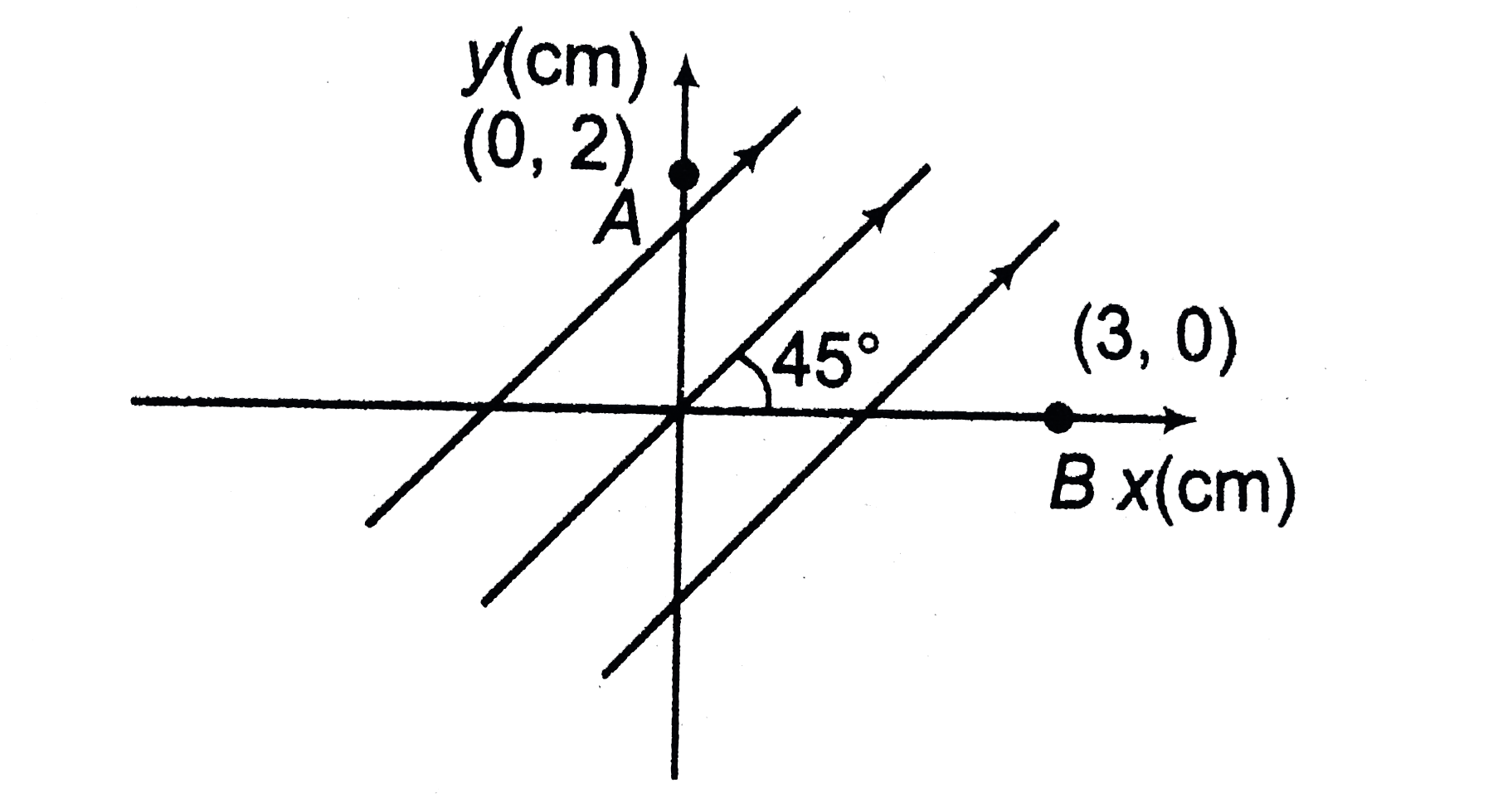
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionA uniform electric field of 100V/m is directed at 3∘ with the positive x-axis as shown in figure. Find the potential difference VBA if OA=2m and OB=4m.

View SolutionA uniform electric field of 100V/m is directed at 30∘ with the positive x-axis as shown in figure. Find the potential difference VBA if OA=2m and OB=4m.

View SolutionA uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View SolutionA uniform electric field of 100 V/m is directed at 30∘ with the positive x-axis as shown in figure Find the potential difference Va−VA if OA = 2 m and OB = 4m.

View SolutionA uniform electric field is present in the positive x - direction. If the intensity of the field is 5NC−1 then find the potential difference (VB−VA) between two points A (0 m, 2 m) and B (5 m, 3 m).
View SolutionIn a certain region, electric field E exists along the x - axis which is uniform. Given B=2√3m and BC=4m. Points A, B, and C are in xy plane.
 .
.
Find the potential difference VA−VB between the points AandB.
View SolutionThe electric field in a certain region is given by E=5ˆi−3ˆjkv/m. The potential difference VB−VA between points a and B having coordinates (4, 0, 3) m and (10, 3, 0) m respectively, is equal to
View Solution
