Two wires A and B made of same material and having their lengths in the ratio 6:1 are connected in series The potential difference across the wire 3V and 2V respectively. If rA and rB are the radii of A and B respectively, then rBrA is
14
12
1
2
The correct Answer is:B
To find the ratio of the radii of two wires A and B connected in series, we will follow these steps:
Step 1: Understand the relationship between voltage, current, and resistance
When two resistors (or wires in this case) are connected in series, the same current flows through both. The potential difference across each wire can be expressed using Ohm's law:
V=I⋅R
where V is the voltage, I is the current, and R is the resistance.
Step 2: Write down the given information
We are given:
- The lengths of the wires A and B are in the ratio 6:1.
- The potential difference across wire A is 3V and across wire B is 2V.
Step 3: Set up the equations for resistance
Let RA and RB be the resistances of wires A and B, respectively. From Ohm's law, we can write:
I⋅RA=3(1)
I⋅RB=2(2)
Step 4: Find the ratio of the resistances
Dividing equation (1) by equation (2):
RARB=32
Step 5: Relate resistance to dimensions
The resistance R of a wire can also be expressed as:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. For a circular wire, the area A can be expressed in terms of the radius r:
A=πr2
Thus, we can write:
RA=ρLAπr2A
RB=ρLBπr2B
Step 6: Substitute into the resistance ratio
Substituting these expressions into the resistance ratio:
ρLAπr2AρLBπr2B=32
The ρ and π cancel out:
LAr2BLBr2A=32
Step 7: Substitute the length ratio
Since the lengths are in the ratio LA:LB=6:1, we can write:
LA=6LB
Substituting this into the equation gives:
6LBr2BLBr2A=32
This simplifies to:
6r2Br2A=32
Step 8: Solve for the ratio of the radii
Cross-multiplying gives:
12r2B=3r2A
Dividing both sides by 3:
4r2B=r2A
Taking the square root:
rBrA=12
Final Answer
Thus, the ratio of the radii rBrA is 12.
---
When two resistors (or wires in this case) are connected in series, the same current flows through both. The potential difference across each wire can be expressed using Ohm's law:
V=I⋅R
where V is the voltage, I is the current, and R is the resistance.
We are given:
- The lengths of the wires A and B are in the ratio 6:1.
- The potential difference across wire A is 3V and across wire B is 2V.
Let RA and RB be the resistances of wires A and B, respectively. From Ohm's law, we can write:
I⋅RA=3(1)
I⋅RB=2(2)
Dividing equation (1) by equation (2):
RARB=32
The resistance R of a wire can also be expressed as:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. For a circular wire, the area A can be expressed in terms of the radius r:
A=πr2
Thus, we can write:
RA=ρLAπr2A
RB=ρLBπr2B
Substituting these expressions into the resistance ratio:
ρLAπr2AρLBπr2B=32
The ρ and π cancel out:
LAr2BLBr2A=32
Since the lengths are in the ratio LA:LB=6:1, we can write:
LA=6LB
Substituting this into the equation gives:
6LBr2BLBr2A=32
This simplifies to:
6r2Br2A=32
Cross-multiplying gives:
12r2B=3r2A
Dividing both sides by 3:
4r2B=r2A
Taking the square root:
rBrA=12
Thus, the ratio of the radii rBrA is 12.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Subjective
53 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two heater wires, made of the same material and having the same length and the same radius, are first connected in series and then in parallel to a constant potential difference. If the rate of heat produced in the two cases are Hs and Hp respectively then HsHp will be
View SolutionFour wires made of same material have different lengths and radii, the wire having more resistance in the following case is
View SolutionTwo wires A and B of same material have radii in the ratio 2:1 and lengths in the ratio 4:1. The ratio of the normal forces required to produce the same change in the lengths of these two wires is
View SolutionTwo wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their resistances,
View SolutionTwo wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their specific resistance.
View SolutionTwo cylindrical conductors A and B of same metallic material have their diameters in the ratio 1:2 and lengths in the ratio 2:1. If the temperature difference between their ends is same, the ratio of heats conducted respectively by A and B per second is,
View SolutionTwo wires 'A' and 'B' of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:1 The two wires are connected in parallel across a battery. The ratio of the heat produced in 'A' to the heat produced in 'B' for the same time is
View SolutionResistance R1and R2, each 60Ω, are connected in series. The Potential difference between points A and B is 120V. Find the reading of voltmeter connected resistance r=120Ω
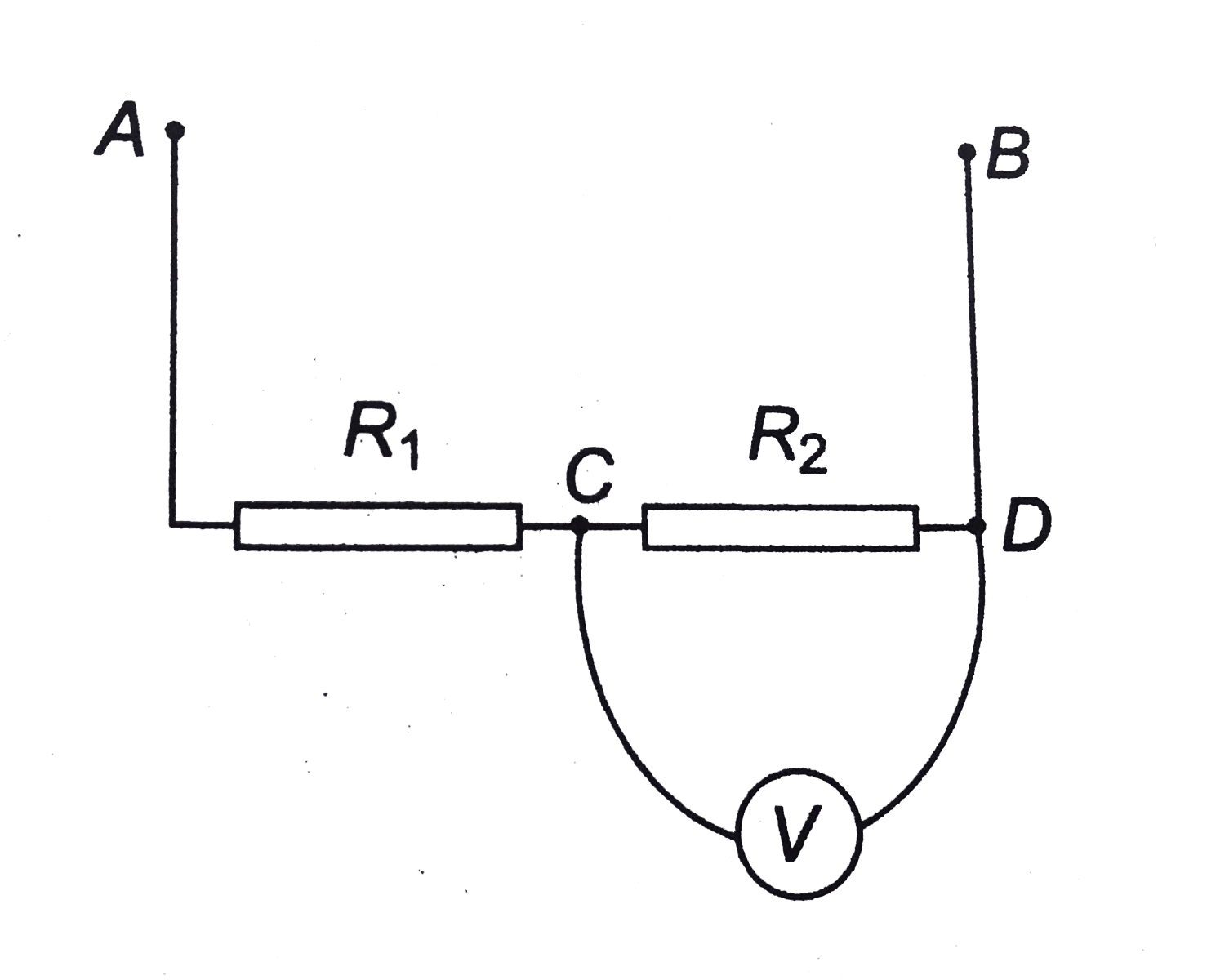
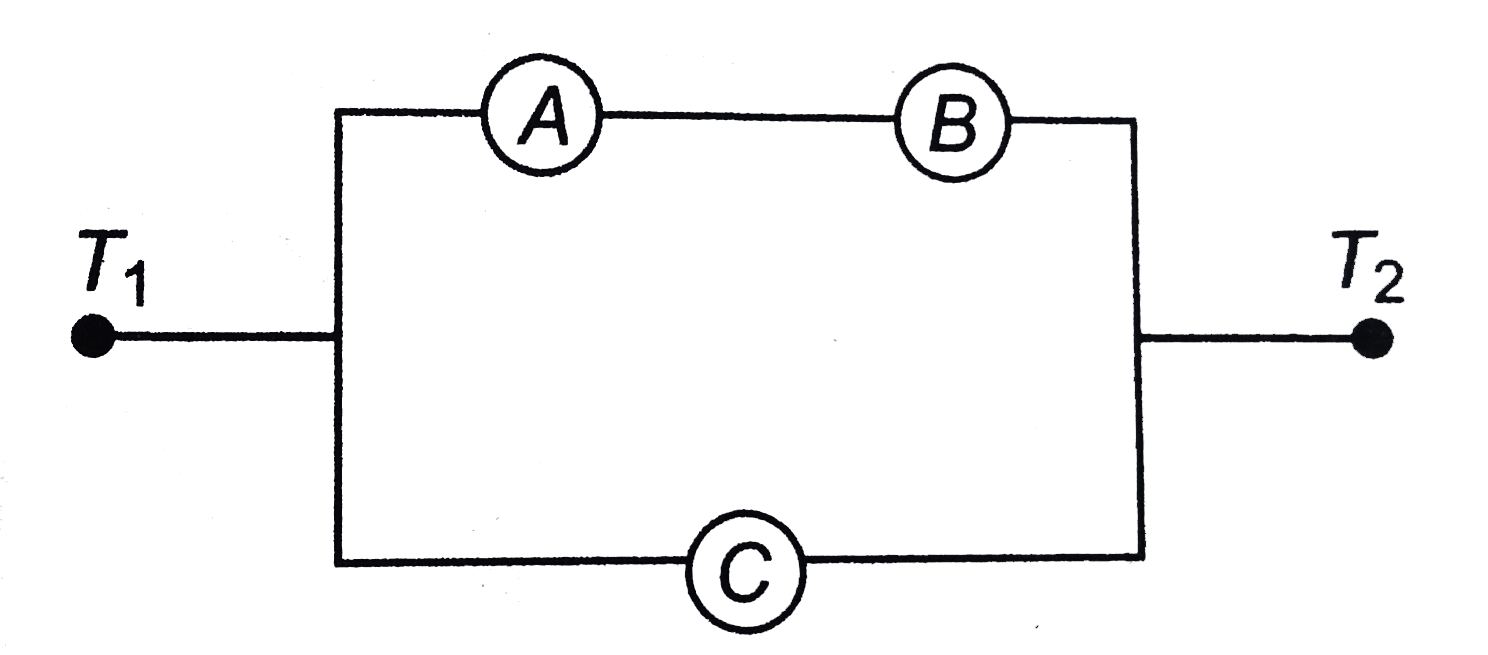
View SolutionThree ammeters A,B, and C of resistances RA,Rb and RC respectively are joined as shown. When some potential difference is appllied across the terminals T1 and T2 their readings are IA,IBandIC respectively Then,
View SolutionTwo, capacitors A and B are connected in series across a 100V supply and it is observed that the potential difference across them are 60V and 40V. A capacitor of 2pF capacitance is now connected in parallel with A and the potential difference across B rises to 90V. Determine the capacitance of A and B
View Solution
