In a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
10cm
20cm
30cm
40cm
The correct Answer is:B
To solve the problem step by step, we will use the principles of a meter bridge and the concept of resistances in a balanced bridge circuit.
Step 1: Understanding the Initial Setup
In the meter bridge, the null point is initially at 20 cm. This means that the lengths of the bridge wire on either side of the null point are:
- Length on one side (L1) = 20 cm
- Length on the other side (L2) = 100 cm - 20 cm = 80 cm
Let the known resistance be R and the unknown resistance be X.
Step 2: Setting Up the Balance Equation
Using the principle of the meter bridge, we can set up the equation based on the lengths:
RX=L1L2=2080
From this, we can simplify:
RX=14
This implies:
X=4R
Step 3: Introducing the Shunt Resistance
Now, when a 10 Ω resistance is shunted across R, the new effective resistance R′ can be calculated using the formula for resistances in parallel:
1R′=1R+110
This can be rearranged to:
R′=R⋅10R+10
Step 4: Analyzing the Shift in Null Point
After shunting the 10 Ω resistance, the null point shifts by 10 cm. The new null point is at:
- New length on one side (L1') = 20 cm - 10 cm = 10 cm
- New length on the other side (L2') = 100 cm - 10 cm = 90 cm
Now we can set up the new balance equation:
R′X=L1′L2′=1090=19
This implies:
R′X=19
Thus:
X=9R′
Step 5: Substituting for R′
We already found that R′=R⋅10R+10. Now substituting this into the equation for X:
X=9(R⋅10R+10)
This simplifies to:
X=90RR+10
Step 6: Equating the Two Expressions for X
From Step 2, we have X=4R. Now we equate the two expressions for X:
4R=90RR+10
Step 7: Solving for R
Cross-multiplying gives:
4R(R+10)=90R
Expanding this:
4R2+40R=90R
Rearranging gives:
4R2−50R=0
Factoring out R:
R(4R−50)=0
Thus, R=0 or R=12.5 Ω.
Step 8: Finding the Unknown Resistance X
Substituting R=12.5 Ω back into the equation for X:
X=4R=4×12.5=50Ω
Final Answer
The unknown resistance X is 50Ω.
---
In the meter bridge, the null point is initially at 20 cm. This means that the lengths of the bridge wire on either side of the null point are:
- Length on one side (L1) = 20 cm
- Length on the other side (L2) = 100 cm - 20 cm = 80 cm
Using the principle of the meter bridge, we can set up the equation based on the lengths:
RX=L1L2=2080
From this, we can simplify:
RX=14
This implies:
X=4R
Now, when a 10 Ω resistance is shunted across R, the new effective resistance R′ can be calculated using the formula for resistances in parallel:
1R′=1R+110
This can be rearranged to:
R′=R⋅10R+10
After shunting the 10 Ω resistance, the null point shifts by 10 cm. The new null point is at:
- New length on one side (L1') = 20 cm - 10 cm = 10 cm
- New length on the other side (L2') = 100 cm - 10 cm = 90 cm
R′X=L1′L2′=1090=19
This implies:
R′X=19
Thus:
X=9R′
We already found that R′=R⋅10R+10. Now substituting this into the equation for X:
X=9(R⋅10R+10)
This simplifies to:
X=90RR+10
From Step 2, we have X=4R. Now we equate the two expressions for X:
4R=90RR+10
Cross-multiplying gives:
4R(R+10)=90R
Expanding this:
4R2+40R=90R
Rearranging gives:
4R2−50R=0
Factoring out R:
R(4R−50)=0
Thus, R=0 or R=12.5 Ω.
Substituting R=12.5 Ω back into the equation for X:
X=4R=4×12.5=50Ω
The unknown resistance X is 50Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Subjective
53 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be

View SolutionFigure 6.32 shows a meter bridge in the (which is nothing but a particle wheastone bridge), consisting of two resistors X and Y together in parellel with a meter long constantan wire of uniform cross section.
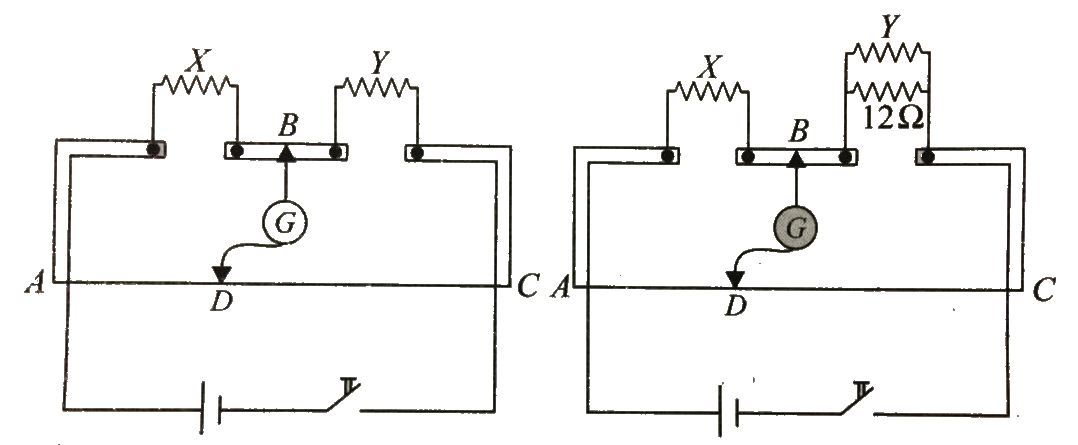
with the help of a movable contact d, one can change the ratio of resistance of the two segments of the wire until a sensitive galvanometer G connected across b and D shows no deflection. The null point is found to be at a distance of 33.7cm. The resistor Y is shunted by a resistance of 12Ω, and the null point is found to shift by a distance of 18.2cm. Determine the resistance of X and Y.
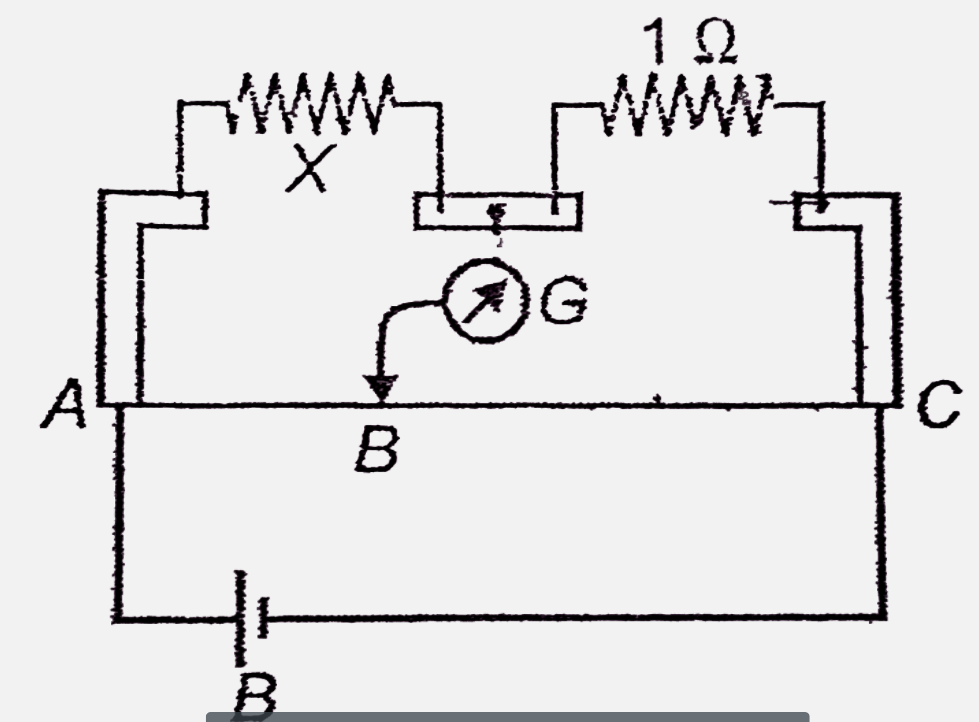
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
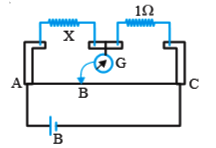
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
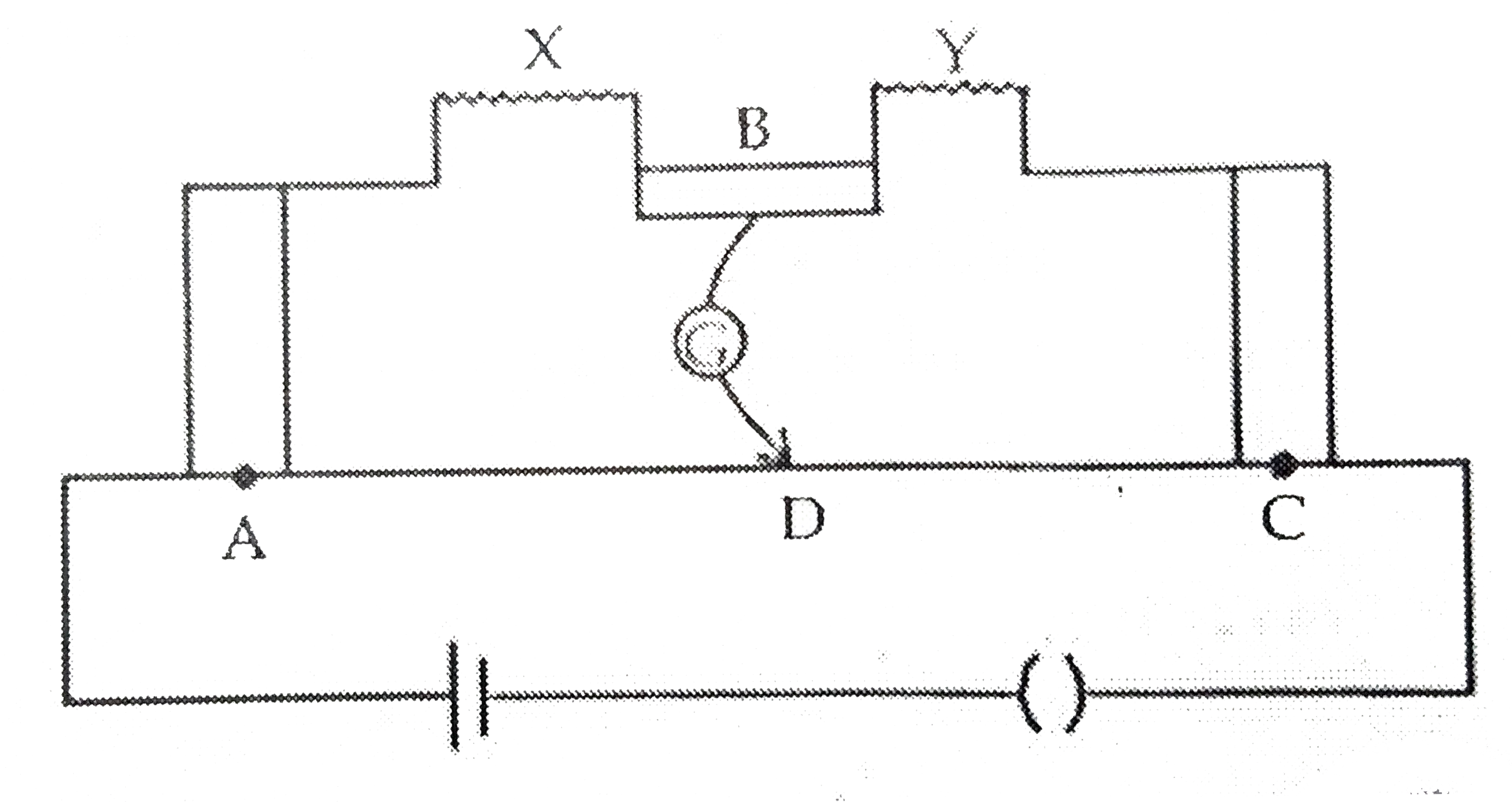
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionIn an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionThe figure
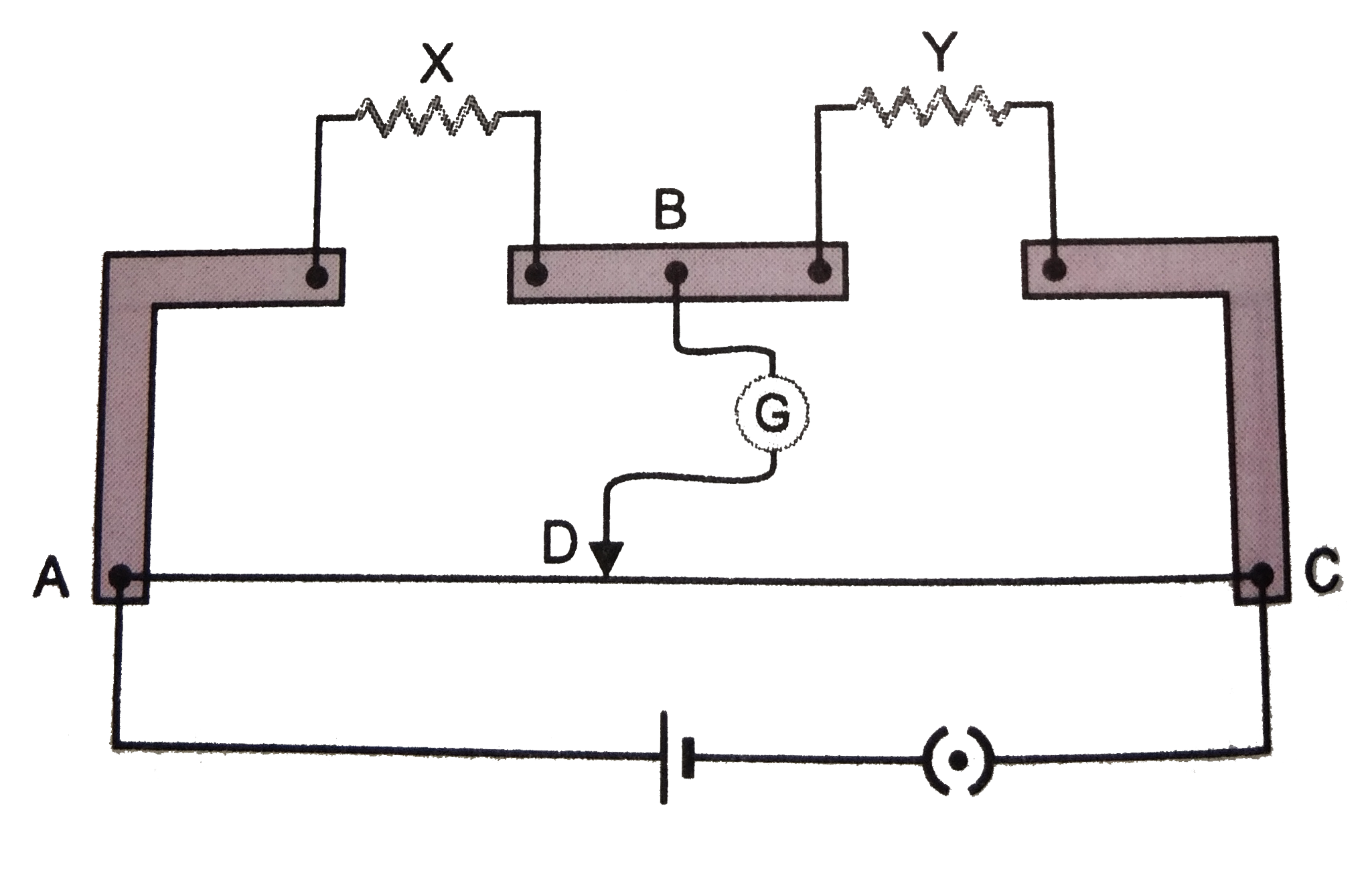
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View Solution
