In a meter bridge experiment, null point is obtained at from one end of the wire when resistance is balanced against another resistance . If , then the new position of the null point from the same end, if one decides to balance a resistance of against will be at.
The correct Answer is:A
To solve the problem, we will use the principles of the meter bridge, which operates on the concept of a Wheatstone bridge. The null point indicates the balance of resistances, and we can derive the new position of the null point when the resistance changes.
1. Understanding the Initial Condition:
- In the first scenario, the null point is obtained at 20cm from one end of the meter bridge wire.
- Let the resistance X be balanced against the resistance Y. According to the meter bridge principle, we have:
\(
\frac{X}{Y} = \frac{L_1}{L_2}
\)
- Here, \(L_1 = 20 \, \text{cm}\) and \(L_2 = 100 \, \text{cm} - L_1 = 80 \, \text{cm}\).
2. Setting Up the Equation:
- Substituting the values into the equation:
\(
\frac{X}{Y} = \frac{20}{80} = \frac{1}{4}
\)
- This implies that:
\(
X = \frac{1}{4}Y \quad \text{or} \quad Y = 4X
\)
3. Changing the Resistance:
- Now, we want to balance a resistance of 4X against Y.
- In this case, we will denote the new position of the null point as \(L\) from the same end of the wire.
4. Setting Up the New Equation:
- The new balance condition can be expressed as:
\(
\frac{4X}{Y} = \frac{L}{100 - L}
\)
- Substituting \(Y = 4X\) into the equation gives:
\(
\frac{4X}{4X} = \frac{L}{100 - L}
\)
- This simplifies to:
\(
1 = \frac{L}{100 - L}
\)
5. Solving for \(L\):
- Cross-multiplying gives:
\(
100 - L = L
\)
- Rearranging this equation results in:
\(
100 = 2L \quad \Rightarrow \quad L = 50 \, \text{cm}
\)
6. Conclusion:
- Therefore, the new position of the null point from the same end is at \(50 \, \text{cm}\).
Final Answer:
The new position of the null point from the same end is at 50 cm.
- In the first scenario, the null point is obtained at 20cm from one end of the meter bridge wire.
- Let the resistance X be balanced against the resistance Y. According to the meter bridge principle, we have:
\(
\frac{X}{Y} = \frac{L_1}{L_2}
\)
- Here, \(L_1 = 20 \, \text{cm}\) and \(L_2 = 100 \, \text{cm} - L_1 = 80 \, \text{cm}\).
- Substituting the values into the equation:
\(
\frac{X}{Y} = \frac{20}{80} = \frac{1}{4}
\)
- This implies that:
\(
X = \frac{1}{4}Y \quad \text{or} \quad Y = 4X
\)
- Now, we want to balance a resistance of 4X against Y.
- In this case, we will denote the new position of the null point as \(L\) from the same end of the wire.
- The new balance condition can be expressed as:
\(
\frac{4X}{Y} = \frac{L}{100 - L}
\)
- Substituting \(Y = 4X\) into the equation gives:
\(
\frac{4X}{4X} = \frac{L}{100 - L}
\)
- This simplifies to:
\(
1 = \frac{L}{100 - L}
\)
- Cross-multiplying gives:
\(
100 - L = L
\)
- Rearranging this equation results in:
\(
100 = 2L \quad \Rightarrow \quad L = 50 \, \text{cm}
\)
- Therefore, the new position of the null point from the same end is at \(50 \, \text{cm}\).
The new position of the null point from the same end is at 50 cm.
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
In the metrebridge experiment , the null point is obtained at N. The value of unkonw resistance X will be .
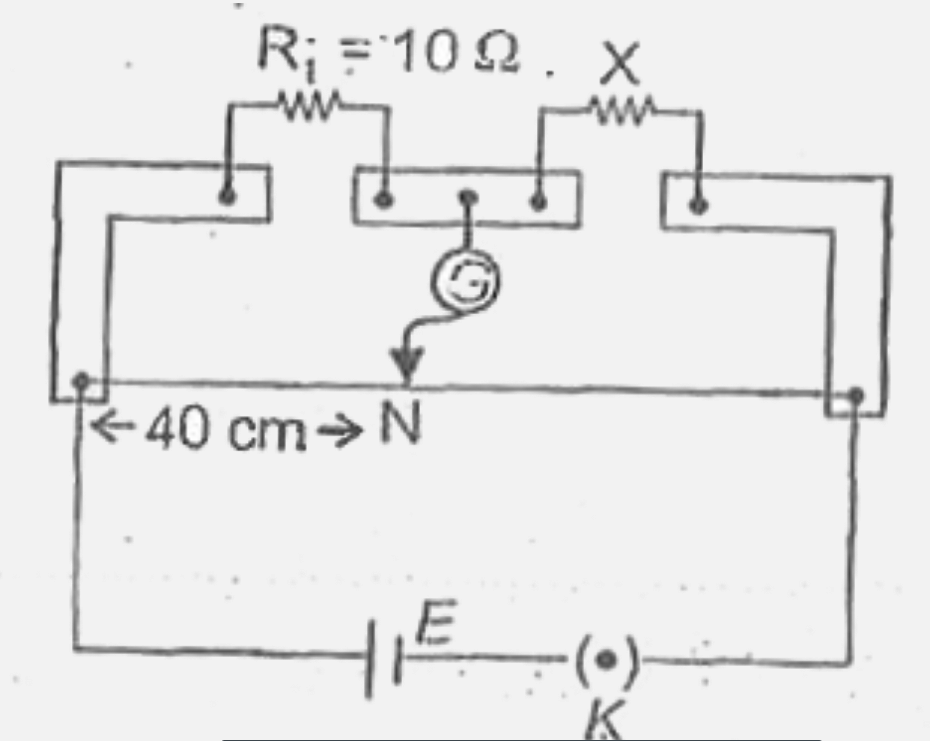
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
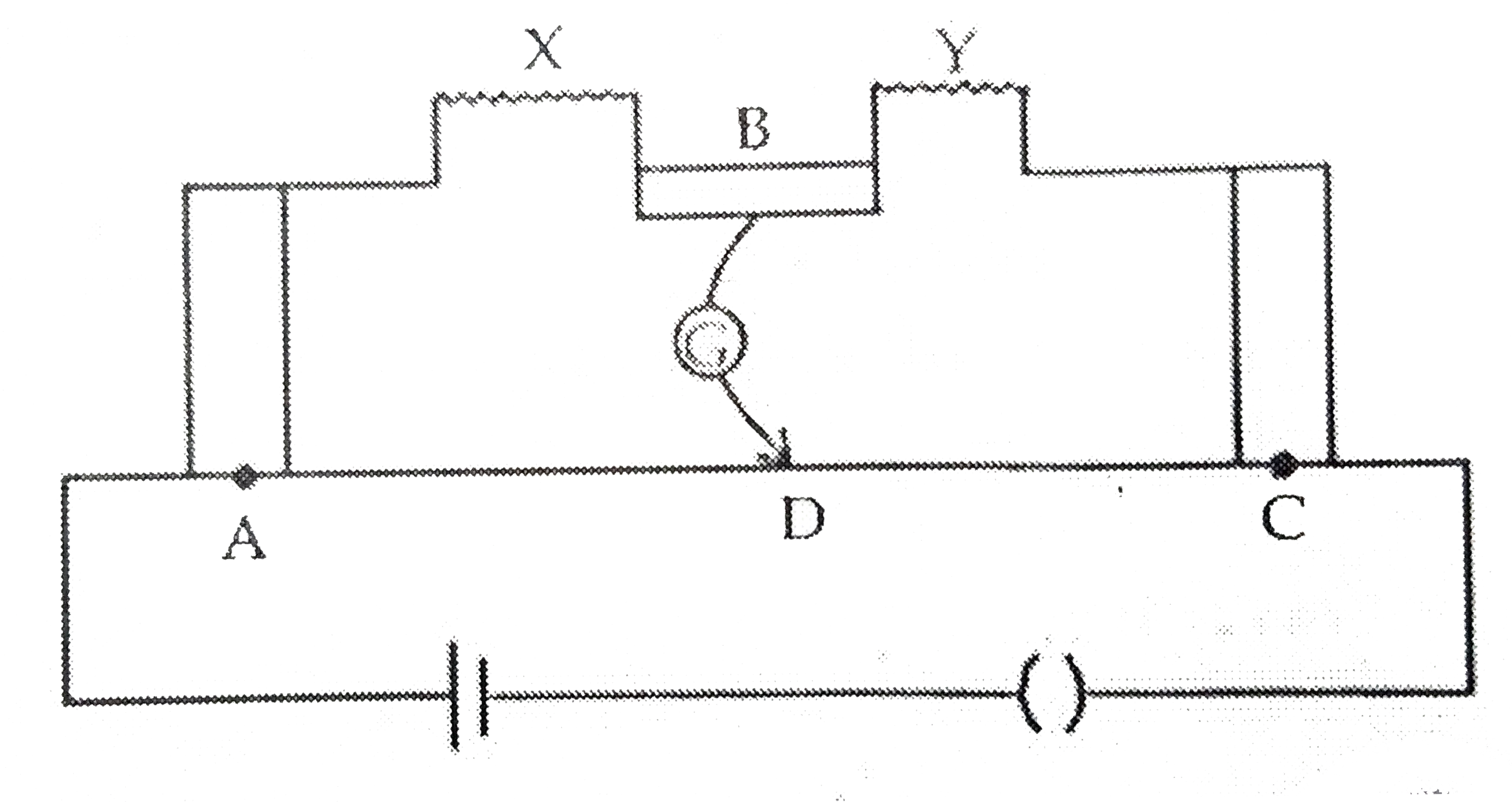
The figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
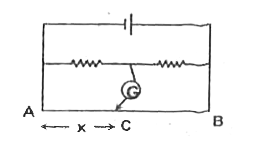
View SolutionIn the meter bridge circuit shown, the null point is obtained at C(AC=x) on the wire AB. If the diameter of the wire AB is doubled, the position of the new null point C' will correspond to
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionStatement-1 : In a Meter Bridge experiment, null point for an unknown resistance is measured. Now, the unknown resistance is put inside an enclosure maintained at a higher temperature. The null point can be obtained at the same point as before by decreasing the value of the standard resistance.
Statement-2 : Resistance of metal increases with increase in temperature.
View SolutionStatement-1 : In a Meter Bridge experiment, null point for an unknown resistance is measured. Now, the unknown resistance is put inside an enclosure maintained at a higher temperature. The null point can be obtained at the same point as before by decreasing the value of the standard resistance.
Statement-2 : Resistance of metal increases with increase in temperature.
View Solution
