A galvanometer of resistance 50Ω is connected to a battery of 3V along with resistance of 2950Ω in series. A full scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 20 division the above series resistance should be
4450Ω
5050Ω
5550Ω
6050Ω
The correct Answer is:A
To solve the problem, we need to find the new series resistance R′ that will reduce the galvanometer's deflection from 30 divisions to 20 divisions.
1. Understanding the Circuit:
The galvanometer has a resistance G=50Ω and is connected in series with a resistor R=2950Ω and a battery of voltage V=3V.
2. Current Calculation for Full Scale Deflection:
The current through the galvanometer when it shows full scale deflection (30 divisions) can be calculated using Ohm's law:
I1=VG+R=350+2950=33000=0.001A
3. Deflection Proportionality:
Since the deflection is proportional to the current, we can express this relationship as:
I1∝30(for 30 divisions)
4. Current Calculation for Reduced Deflection:
We want to find the new current I2 that corresponds to a deflection of 20 divisions:
I2∝20
5. Setting Up the Equations:
We can set up the following equations based on the proportionality of current to deflection:
I1I2=3020⟹I2=23I1
6. Substituting for I2:
Substitute I1 into the equation:
I2=23×0.001=23000=0.0006667A
7. Finding the New Resistance R′:
Now we can write the equation for the new current I2 with the new resistance R′:
I2=VG+R′⟹0.0006667=350+R′
8. Rearranging the Equation:
Rearranging gives:
50+R′=30.0006667⟹50+R′=4500
9. Solving for R′:
R′=4500−50=4450Ω
Final Answer:
The resistance that should be connected in series to reduce the deflection to 20 divisions is R′=4450Ω.
The galvanometer has a resistance G=50Ω and is connected in series with a resistor R=2950Ω and a battery of voltage V=3V.
The current through the galvanometer when it shows full scale deflection (30 divisions) can be calculated using Ohm's law:
I1=VG+R=350+2950=33000=0.001A
Since the deflection is proportional to the current, we can express this relationship as:
I1∝30(for 30 divisions)
We want to find the new current I2 that corresponds to a deflection of 20 divisions:
I2∝20
We can set up the following equations based on the proportionality of current to deflection:
I1I2=3020⟹I2=23I1
Substitute I1 into the equation:
I2=23×0.001=23000=0.0006667A
Now we can write the equation for the new current I2 with the new resistance R′:
I2=VG+R′⟹0.0006667=350+R′
Rearranging gives:
50+R′=30.0006667⟹50+R′=4500
R′=4500−50=4450Ω
The resistance that should be connected in series to reduce the deflection to 20 divisions is R′=4450Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Level 2 More Than One Correct
Explore 10 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Level 2 Comprehension Example Type
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Level 1 Subjective
Explore 53 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
A galvanometer of resistance 50Ω is connected to a battery of 3V along with a resistance of 2950Ω in series. A full scale deflection of 30 division is obtained in the galvanometer. In order to reduce this deflection to 20 division, the resistance in series should be:-
View SolutionA galvanometer of resistance 50Ω is connected to a battery of 8 V along with a resistance of 3950Ω in series. A full scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 15 divisions, the resistance in series should be .... Ω.
View Solution
Knowledge Check
A galvanometer of resistance 25Ω is connected to a battery of 2 volt along with a resistance in series. When the value of this resistance is 3000Ω, a full scale deflection of 30 units is obtained in the galvanometer. In order to reduce this deflection to 20 units, the resistance in series will be
A4512ΩB5413ΩC2000ΩD6000Ω
A galvanometer of resistance 30Ω is connected to a battery of emf 2 V with 1970Ω resistance in series. A full scale deflection of 20 divisions is obtained in the galvanometer. To reduce the deflection to 10 divisions, the resistance in series required is
View SolutionA galvanometer of 50Ω resistance when connected across the terminals of a battery of emf 2V along with the resistance 200Ω the deflection produced in the galvanometer is 10 divisions. If the total number of divisions on the galvanometer ·scale on either side of central zero is 30, then the maximum current that can pass through the galvanometer is
View SolutionA galvanometer having internal resistance 10Ω required 0.01 A for a full scale deflection. To convert this galvanometer to a voltmeter of full scale deflection at 120 V, we need to connect a resistance of
View SolutionTo measure the resistance of a galvanometer by half deflection method, a shunt is connected to the galvanometer . The shunt is
View SolutionA galvanometer of resistance 50Ω is converted into an ammeter by connecting a low resistance (shunt) of value 1Ω in parallel to the galvanometer, S. If full - scale deflection current of the galvanometer is 10 mA, then the maximum current that can be measured by the ammeter is -
View SolutionA galvanometer has resistance 1Ω. Maximum deflection current through it is 0.1 A
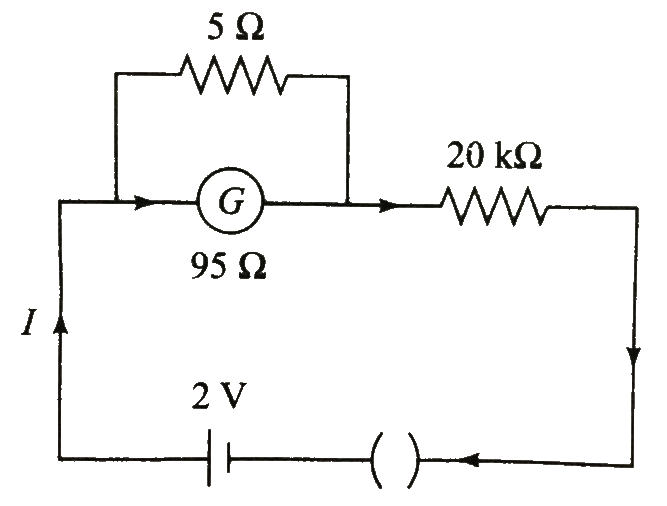
View SolutionA galvanometer of resistance 95Ω, shunted resistance of 5Ω, gives a deflection of 50 divisions when joined in series with a resistance of 20kΩ and a 2V accumulator. What is the current sensitivity of the galvanomter (in div/μA)?
View Solution