An ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are , , and respectively. The corresponding quantities of work involved are , , and respectively.
(a) Find the value of .
(b) What is the efficiency of the cycle?
The correct Answer is:A, B
To solve the problem step-by-step, we will follow the principles of thermodynamics, specifically applying the first law of thermodynamics to a cyclic process.
Step 1: Understand the First Law of Thermodynamics
The first law of thermodynamics states that:
ΔQ=ΔU+ΔW
For a cyclic process, the change in internal energy (ΔU) is zero, hence:
Qnet=Wnet
Step 2: Calculate the Net Heat Transfer
The net heat transfer (Qnet) for the cycle can be calculated by summing the heat transfers for each step:
Qnet=Q1+Q2+Q3+Q4
Substituting the given values:
Qnet=5960J−5585J−2980J+3645J
Calculating this gives:
Qnet=5960−5585−2980+3645=1040J
Step 3: Calculate the Net Work Done
Similarly, the net work done (Wnet) can be expressed as:
Wnet=W1+W2+W3+W4
Substituting the known values:
Wnet=2200J−825J−1100J+W4
This simplifies to:
Wnet=2200−825−1100+W4=275+W4
Step 4: Set Up the Equation
From the first law, we know:
Qnet=Wnet
Substituting the expressions from Steps 2 and 3:
1040J=275J+W4
Step 5: Solve for W4
Rearranging the equation to find W4:
W4=1040J−275J=765J
Step 6: Calculate the Efficiency of the Cycle
The efficiency (η) of the cycle is given by:
η=WnetQabsorbed×100
Where Qabsorbed is the sum of the heat absorbed during the process:
Qabsorbed=Q1+Q4=5960J+3645J=9605J
Now substituting the values:
η=1040J9605J×100
Calculating this gives:
η≈10.82%
Final Answers:
(a) The value of W4 is 765J.
(b) The efficiency of the cycle is approximately 10.82%.
The first law of thermodynamics states that:
ΔQ=ΔU+ΔW
For a cyclic process, the change in internal energy (ΔU) is zero, hence:
Qnet=Wnet
The net heat transfer (Qnet) for the cycle can be calculated by summing the heat transfers for each step:
Qnet=Q1+Q2+Q3+Q4
Substituting the given values:
Qnet=5960J−5585J−2980J+3645J
Calculating this gives:
Qnet=5960−5585−2980+3645=1040J
Similarly, the net work done (Wnet) can be expressed as:
Wnet=W1+W2+W3+W4
Substituting the known values:
Wnet=2200J−825J−1100J+W4
This simplifies to:
Wnet=2200−825−1100+W4=275+W4
From the first law, we know:
Qnet=Wnet
Substituting the expressions from Steps 2 and 3:
1040J=275J+W4
Rearranging the equation to find W4:
W4=1040J−275J=765J
The efficiency (η) of the cycle is given by:
η=WnetQabsorbed×100
Where Qabsorbed is the sum of the heat absorbed during the process:
Qabsorbed=Q1+Q4=5960J+3645J=9605J
Now substituting the values:
η=1040J9605J×100
Calculating this gives:
η≈10.82%
(a) The value of W4 is 765J.
(b) The efficiency of the cycle is approximately 10.82%.
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 1
2 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 2
1 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
An ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are Q1=5960J,Q2=−5585J,Q3=−2980JandQ4=3645J, respectively. The corresponding quantities of work involved are W1=2200J,W2=−825J,W3=−1100JandW4 respectively.
(1) Find the value of W4.
(2) What is the efficiency of the cycle
View SolutionAn ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are Q1=5960J,Q2=−5585J,Q3=−2980JandQ4=3645J, respectively. The corresponding quantities of work involved are W1=2200J,W2=−825J,W3=−1100JandW4 respectively.
(1) Find the value of W4.
(2) What is the efficiency of the cycle
View SolutionAn ideal gas is taken through a cyclic thermodynamical process through four steps. The amounts of heat involved in these steps areQ1=5960J,Q2=−5585J,Q3=−2980J,Q4=3645J, respectively . The corresponding works involved are W1=2200J,W2=−825J,W3=−1100J,W4 respectively. The value of W4 is
View SolutionAn ideal gas is taken through a cyclic thermodynamics process through four steps. The amount of heat given to the system in these steps are Q1=1000J, Q2=−800J, Q3=450J, Q4=−200J respectively. The efficiency of cycle is nearly
View SolutionA gas is taken through a cyclic process ABCA as shown in, if 2.4 cal of heat is given in the process, what is the value of J ?
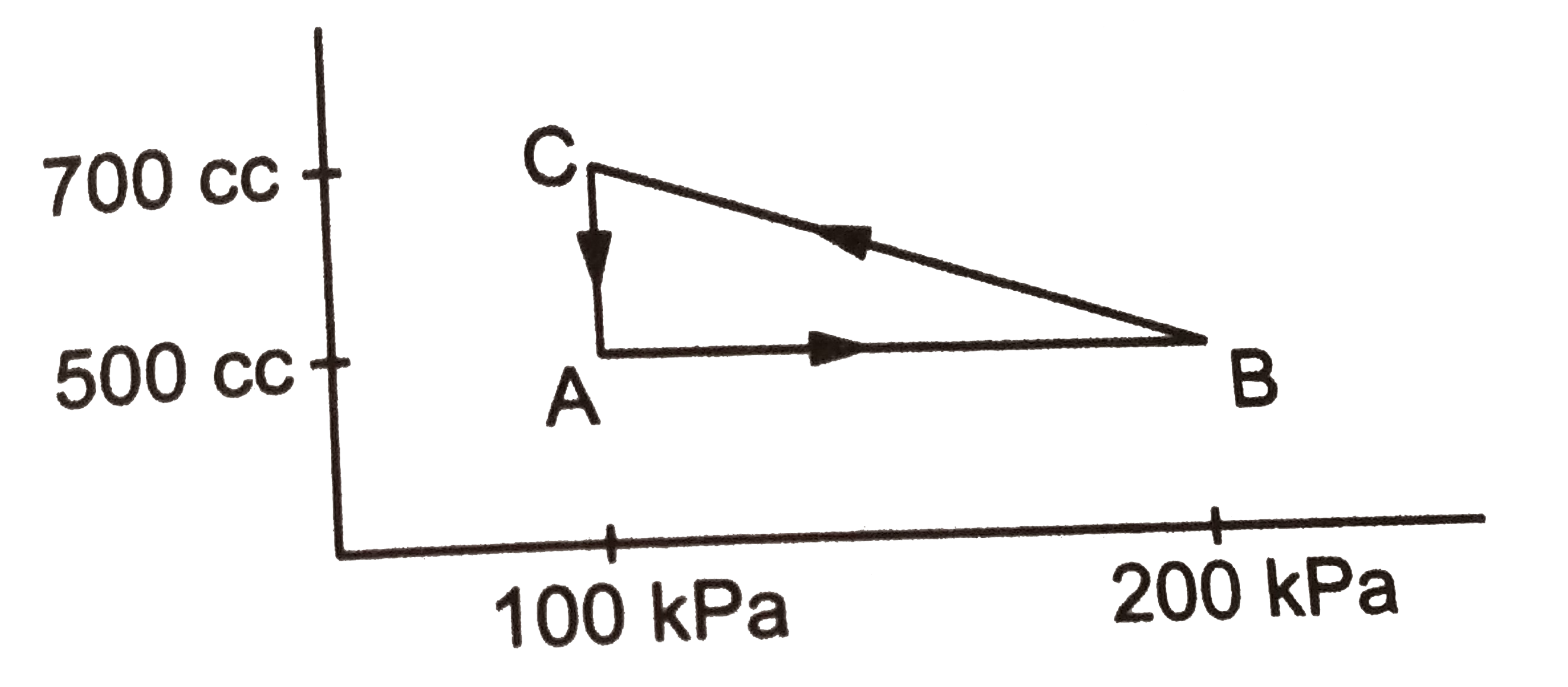
View SolutionA gas is taken through a cyclic process ABCA as shown in, if 2.4cal of heat is given in the process, what is the value of J ?

View SolutionA cyclic process contains four steps AB,BC,CD and DA. Heat involved in different processes is given as QAB=+200J,QBC=+600J,QCD=−300J,QDA=0, then efficiency of process is
View SolutionA gas undergoes A to B through three different processes 1,2 and 3 as shown in the figure. The heat supplied to the gas is Q1, Q2 and Q3 respectively, then

View SolutionDuring an isobaric heating process the work done by oxygen gas is 4 J. Calculate the amount of heat transferred to the gas. [γ=1.4]
View SolutionEfficiency of cyclic process is 50% if heat Q1=1915J , Q2=−40J , Q3=125J, then Q4 is unknown then find the value of Q4.
View Solution
