During an isobaric heating process the work done by oxygen gas is 4 J. Calculate the amount of heat transferred to the gas. [γ=1.4]
To solve the problem, we will use the first law of thermodynamics, which states:
Q=ΔU+W
Where:
- Q is the heat added to the system,
- ΔU is the change in internal energy,
- W is the work done by the system.
Step 1: Identify the known values
From the problem, we know:
- Work done by the gas, W=4J
- The specific heat ratio, γ=1.4
Step 2: Relate change in internal energy to temperature change
For an ideal gas undergoing an isobaric process, the change in internal energy can be expressed as:
ΔU=nCVΔT
Where:
- CV is the specific heat at constant volume.
Using the relationship between CV and CP (specific heat at constant pressure), we have:
CP=CV+R
And for an ideal gas, we can express CV in terms of R and γ:
CV=Rγ−1
Step 3: Substitute CV into the internal energy equation
Substituting CV into the equation for ΔU:
ΔU=n(Rγ−1)ΔT
Step 4: Use the ideal gas law to express nRΔT
From the ideal gas law, we know:
PV=nRT⟹nRΔT=PΔV
Step 5: Substitute nRΔT into the equation for ΔU
Thus, we can express ΔU as:
ΔU=PΔVγ−1
Step 6: Substitute ΔU back into the first law of thermodynamics
Now, substituting ΔU into the first law equation:
Q=ΔU+W=PΔVγ−1+W
Step 7: Substitute W and simplify
Since W=PΔV:
Q=PΔVγ−1+PΔV
Factoring out PΔV:
Q=PΔV(1γ−1+1)
Step 8: Simplify the expression
This can be simplified to:
Q=PΔV(1+(γ−1)γ−1)=PΔV(γγ−1)
Step 9: Relate it back to the work done
Since PΔV=W:
Q=W(γγ−1)
Step 10: Substitute the known values
Now substituting W=4J and γ=1.4:
Q=4(1.41.4−1)=4(1.40.4)=4×3.5=14J
Final Answer
The amount of heat transferred to the gas is:
14J
- Q is the heat added to the system,
- ΔU is the change in internal energy,
- W is the work done by the system.
From the problem, we know:
- Work done by the gas, W=4J
- The specific heat ratio, γ=1.4
For an ideal gas undergoing an isobaric process, the change in internal energy can be expressed as:
- CV is the specific heat at constant volume.
Substituting CV into the equation for ΔU:
From the ideal gas law, we know:
Thus, we can express ΔU as:
Now, substituting ΔU into the first law equation:
Since W=PΔV:
This can be simplified to:
Since PΔV=W:
Now substituting W=4J and γ=1.4:
The amount of heat transferred to the gas is:
Topper's Solved these Questions
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SOLVED EXAMPLES
9 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - ADDITIONAL SOLVED PROBLEMS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
Similar Questions
In a isobaric process the work done by a di-atomic gas is 10 J , the heat given to the gas will be :
View SolutionAn ideal gas of adiabatic exponent γ is expanded so that the amount of heat transferred to the gas is equal to the decrease of its internal energy. Then, the equation of the process in terms of the variables T and V is
View Solution
Knowledge Check
In the P-V diagram (Fig 15.14.1) given below, three thermodynamic processes occur for an ideal gas. Processes 1→2,2→3and3→1 are isothermal, isochoric and adiabatic processes respectively. The total amt of work done is 10 J. During the process 3→1, 20 J of work is done on the system. The amount of heat added to the system during the process 1→2 is
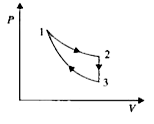 A30 JB20 JC10 JD0 J
A30 JB20 JC10 JD0 J
In isobaric process of ideal gas (f=5) work done by gas is equal of 10J. Then heat given to gas during process:
View SolutionStatement 1: Heat supplied to a gas is process is 100 J and work done by the gas in the same process is 120 J, then pressure of he gas in the process should increase.
because
Statement2: Work done by the gas is greater than the heat supplied to the gas. Hence, internal energy of the gas should decrease.
View SolutionIn a given process work done on a gas is 40 J and increase in its internal energy is 10J. Find heat given or taken to/from the gas in this process.
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View SolutionDuring an expansion of ideal gas the work done by gas is 100J and the heat capacity to process is found to be +2J/∘C. Find ΔE fo gas if the final temperature of gas is 25∘C higher than its initial temperature.
View SolutionIn an isobaric process, heat is supplied to a monoatomic ideal gas. The fraction of heat that goes itno mechanical work is
View SolutionOne mole of an ideal gas is heated isobarically from the freezing point to the boiling point of water, each under normal pressure. Find out the work done by the gas and the change in its internal energy. The amount of heat involved is 1 kJ. Given gas constant R= 8.3 J/mol K.
View Solution
