Pressure p, volume V and temperature T for a certain gas are related by
p=αT−βT2V
where, α and β are constants. Find the work done by the gas if the temperature changes from T1 to T2 while the pressure remains the constant.
The correct Answer is:A, B
To solve the problem, we need to find the work done by the gas when the temperature changes from T1 to T2 while keeping the pressure constant. The relationship between pressure p, volume V, and temperature T is given by:
p=αT−βT2V
Step 1: Rearranging the Equation
We can rearrange the equation to express volume V in terms of pressure p and temperature T:
V=αT−βT2p
Step 2: Differentiating Volume with Respect to Temperature
Next, we differentiate V with respect to T:
dV=ddT(αT−βT2p)
Using the quotient rule, we find:
dV=1p(α−2βT)dT
Step 3: Work Done by the Gas
The work done W by the gas during this process, when pressure is constant, is given by the integral of p with respect to V:
W=∫pdV
Substituting the expression for dV:
W=∫p(α−2βTp)dT
The p cancels out:
W=∫(α−2βT)dT
Step 4: Integrating
Now we integrate from T1 to T2:
W=(αT−βT2)T2T1
Step 5: Evaluating the Integral
Evaluating the integral at the limits T1 and T2:
W=(αT2−βT22)−(αT1−βT21)
This simplifies to:
W=α(T2−T1)−β(T22−T21)
Final Answer
Thus, the work done by the gas is:
W=α(T2−T1)−β(T22−T21)
---
We can rearrange the equation to express volume V in terms of pressure p and temperature T:
Next, we differentiate V with respect to T:
The work done W by the gas during this process, when pressure is constant, is given by the integral of p with respect to V:
Now we integrate from T1 to T2:
Evaluating the integral at the limits T1 and T2:
Thus, the work done by the gas is:
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Passage II
3 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
Pressure P, Volume V and temperature T of a certain material are related by the P=αT2V. Here α is constant. Work done by the material when temparature changes from T0 to 2T0 while pressure remains constant is :
View SolutionTemperature of two moles of an ideal gas is increased by 300K in a process V=aT, where a is positive constant. Find work done by the gas in the given process.
View Solution
Knowledge Check
Pressure P, volume V and temperature T for a certain gas are related by P=AT−BT2V, where A and B are constatns .The work done by the gas as its temperature change from T1 to T2 while pressure remaining constatn is
AA−B2(R2−T1)BA(T2−T1)−B(T22−T21)CA2(T22−T21)−B3(T32−T31)DA(T2−T1)−B3(T2−T1)3The temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P=aT−1 where a is a constant .Then the work done by the gas is
Aa. nRTBb. 4nRTCc. 2nRTDd. 6nRT
n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionIn an adiabatic change, the pressure p and temperature T of a diatomic gas are related by the relation p∝Tα, where α equals
View SolutionThe temperature (T) of one mole of an ideal gas varies with its volume (V) as T=−αV3+βV2, where αandβ are positive constants. The maximum pressure of gas during this process is
View SolutionThe volume V versus temperature T graphs for a certain amount of a perfect gas at two pressure p1andp2 are as shown in Fig. It follows from the graphs that p1 is greater than p2.
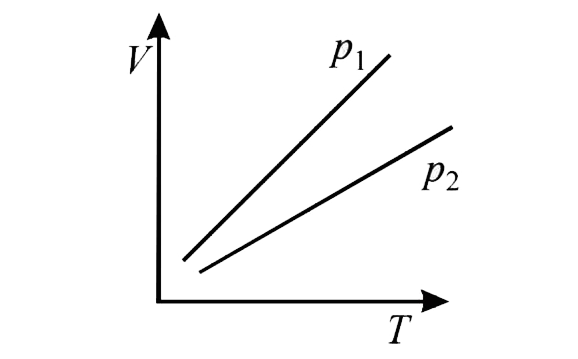
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionThe volume V versus temperature T graphs for a certain amount of a perfect gas at two pressure p1andp2 are as shown in Fig. Show that p1 is less than p2.

View Solution
