A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
The correct Answer is:C, D
Fraction of volume immersed before putting the new weigh =ρblockρwater=8001000=0.8
i.e. 20% of3cm or 0.6cm is above water. Let w is the new weight, then spring will be compressed by 0.6cm
∴w+weight of block=Upthrust on whole
volume of block + spring force
or, w=(3×10−2)3×1000×10+50×
(0.6×10−2)=(3×10−2)3×800×10
∴w=0.354N.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.1
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.2
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cubical block of side 0.5 M floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take density of water =103kg/m3]
View SolutionA cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
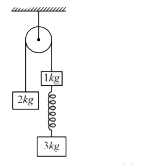
View SolutionFrom the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
View SolutionA capillary tube of radius 0.20 mm is dipped vertically in water. Find the height of the water column raised in the tube. Surface tension of water =0.075Nm−1 and density of water =1000kgm−3.Takeg=10ms−2.
View SolutionFind the ratio of the weights, as measured by a spring balance, of a 1 kg block of iron and a 1kg block of wood. Density of iron =7800kgm−3 density of wood =800kgm−3 and density of air =1.293kgm−3.
View SolutionA cubic block of side a is connected with two similar vertical springs as shown. Initially, bottom surface of the block of density σ touches the surface of the fluid of density 2σ while floating. A weight is placed on the block so that it is immersed half in the fluid, find the weight.

View SolutionA particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretched by 0.20 cm. Take g=π2ms−2
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

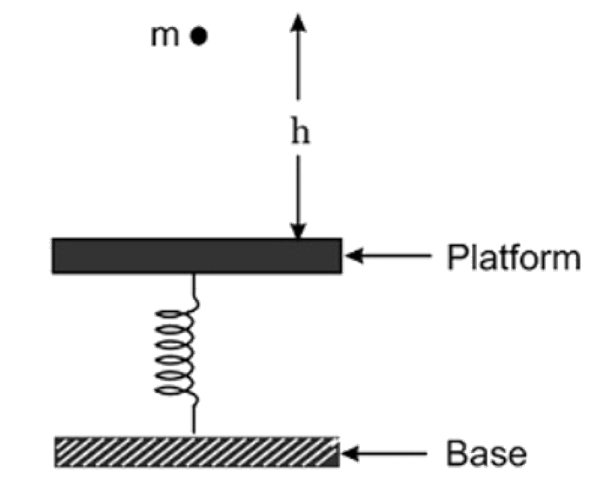
View SolutionA particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)
View Solution
