The topmost and bottommost velocities of a disc are v1 and v2(<v1 in the same direction. The radius is R. Find te value of angular velocity ω.
To solve the problem, we need to find the angular velocity ω of a disc given the topmost velocity v1 and the bottommost velocity v2 of the disc, where v2<v1 and both velocities are in the same direction. The radius of the disc is R.
1. Understand the Motion of the Disc:
- The disc is undergoing both rotational and translational motion. The point at the bottommost position (let's call it point P) and the point at the topmost position (let's call it point Q) will have different velocities due to this combined motion.
2. Define the Velocities:
- Let v be the translational velocity of the center of mass of the disc.
- The velocity of point P (bottommost point) can be expressed as:
v2=v−ωR
- The velocity of point Q (topmost point) can be expressed as:
v1=v+ωR
3. Set Up the Equations:
- From the definitions above, we have two equations:
v2=v−ωR(1)
v1=v+ωR(2)
4. Subtract the Two Equations:
- To eliminate v from the equations, subtract equation (1) from equation (2):
v1−v2=(v+ωR)−(v−ωR)
- Simplifying this gives:
v1−v2=2ωR
5. Solve for Angular Velocity ω:
- Rearranging the equation to solve for ω:
ω=v1−v22R
Final Answer:
ω=v1−v22R
- The disc is undergoing both rotational and translational motion. The point at the bottommost position (let's call it point P) and the point at the topmost position (let's call it point Q) will have different velocities due to this combined motion.
- Let v be the translational velocity of the center of mass of the disc.
- The velocity of point P (bottommost point) can be expressed as:
v2=v−ωR
- The velocity of point Q (topmost point) can be expressed as:
v1=v+ωR
- From the definitions above, we have two equations:
v2=v−ωR(1)
v1=v+ωR(2)
- To eliminate v from the equations, subtract equation (1) from equation (2):
v1−v2=(v+ωR)−(v−ωR)
- Simplifying this gives:
v1−v2=2ωR
- Rearranging the equation to solve for ω:
ω=v1−v22R
ω=v1−v22R
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Two points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction. Separated by a distance r. Then the angular velocity of the rod is :
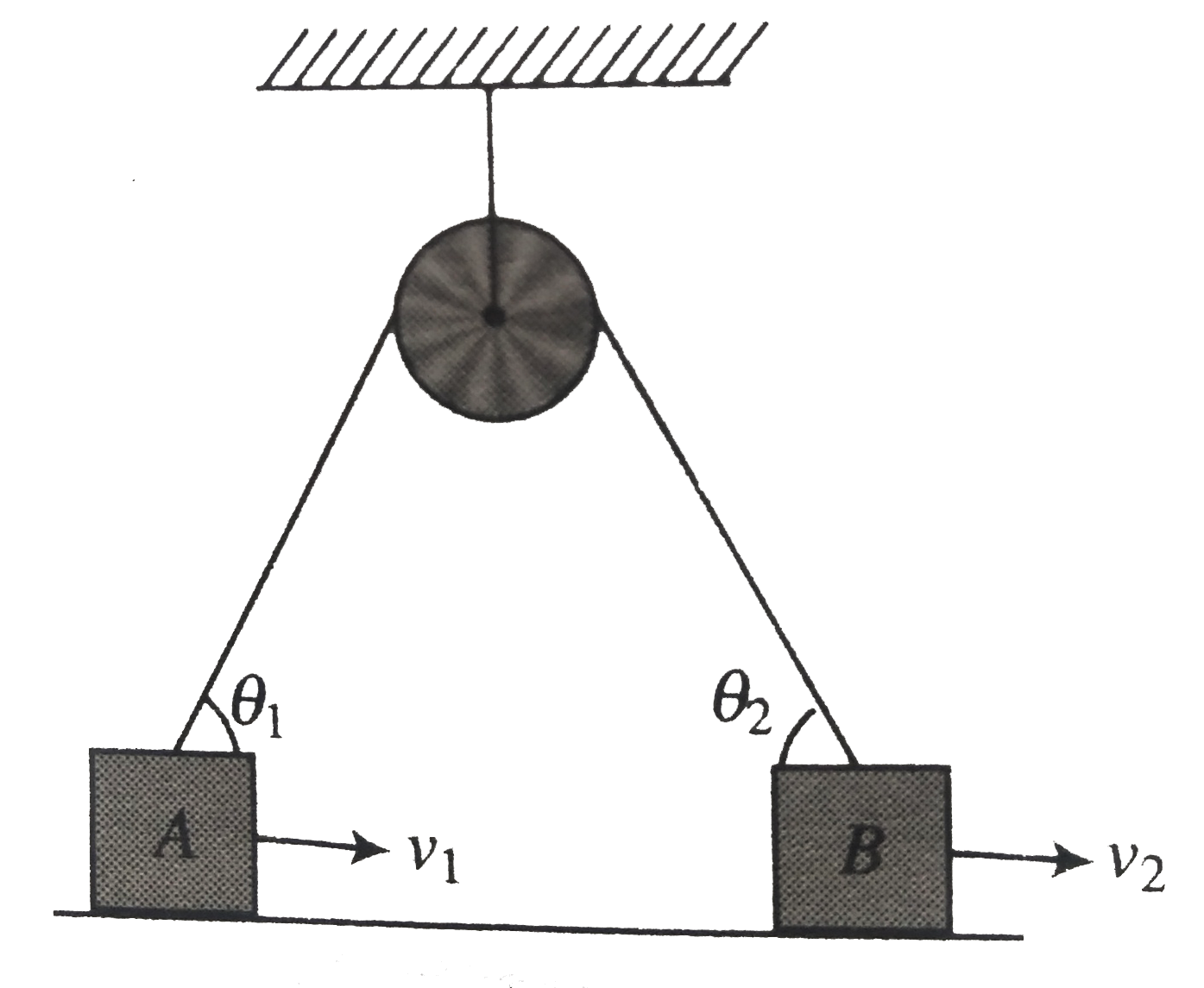
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
View Solution
Knowledge Check
A particle is moving in a circular orbit of radius r1 with an angular velocity ω1. It jumps to another circular orbit of radius r2 and attains an angular velocity ω2. IF r2=0.5r1 and assuming that no external torque is applied to that system, then, the angular velocity ω2 is given by
Aω2=4ω1Bω2=3ω1Cω2=2ω1Dω2=ω1
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

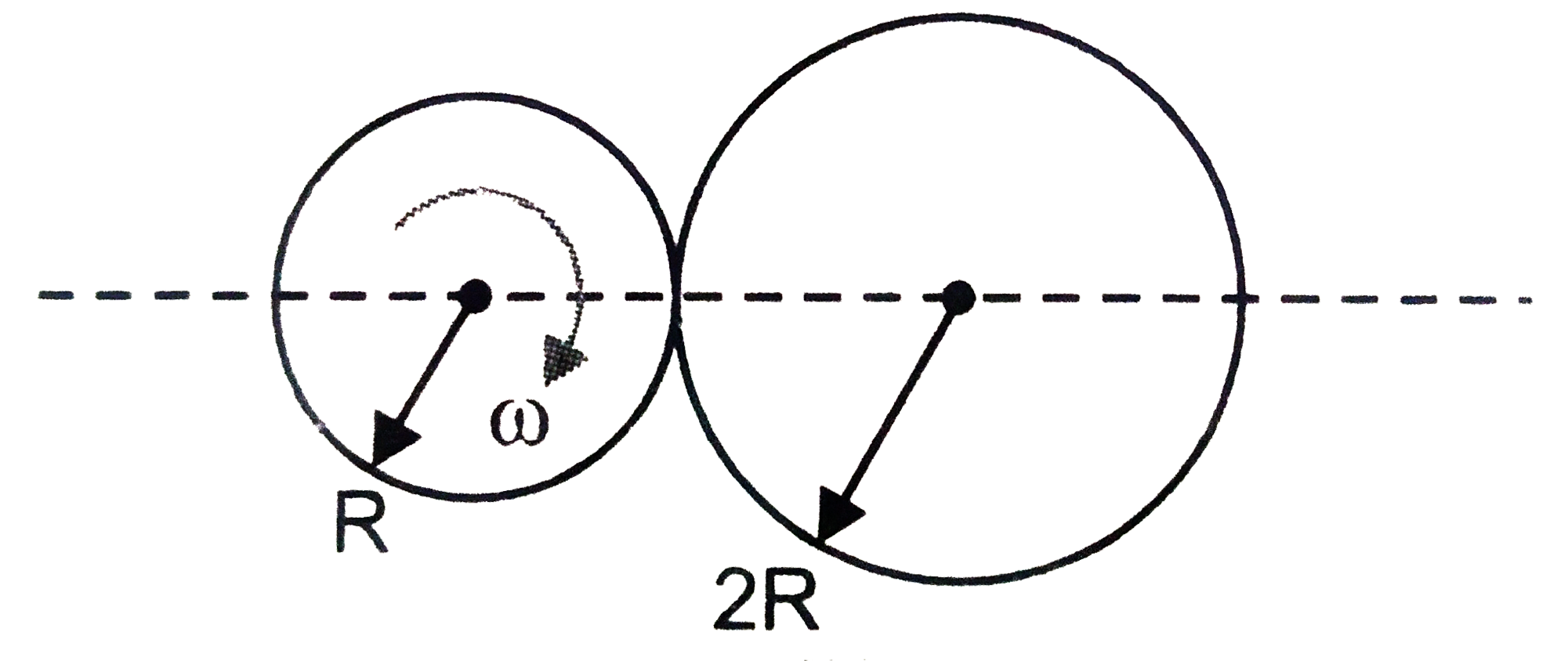
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionA disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionA uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, spectively. Find the
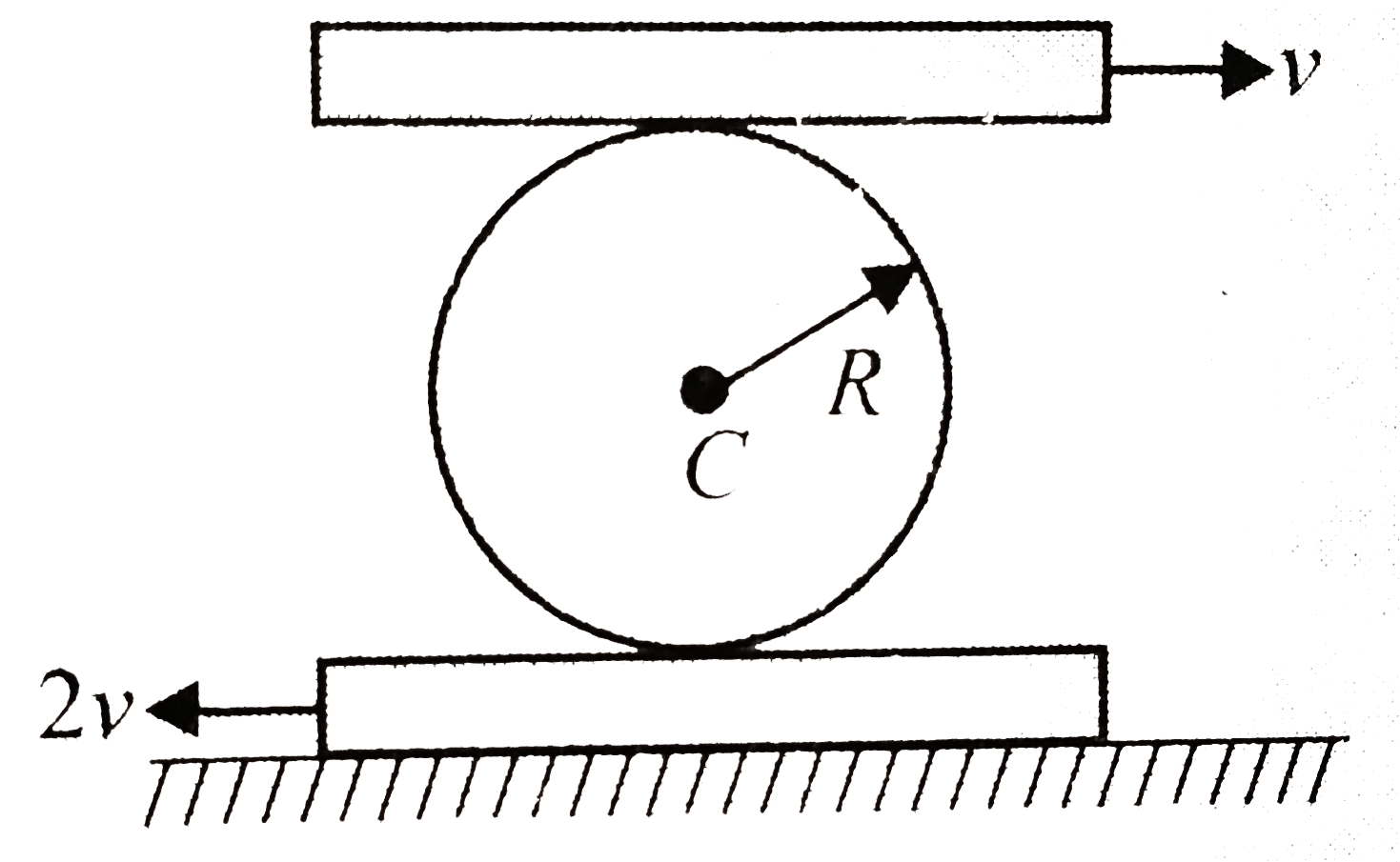
a. velocity of CM of the disc.
b. angular velocity of the disc.
View Solution
