A circular lamina of radius a and centre O has a mass per unit area of kx2, where x is the distance from O and k is a constant. If the mass of the lamina is M, find in terms of M and a, the moment of inertia of the lamina about an axis through O and perpendicular to the lamina.
To find the moment of inertia I of a circular lamina of radius a and mass per unit area given by kx2, we can follow these steps:
Step 1: Define the mass element
The mass per unit area of the lamina is given by σ=kx2, where x is the distance from the center O. The area element in polar coordinates is given by dA=rdrdθ.
Step 2: Express the mass element
The mass element dm can be expressed as:
dm=σdA=kx2dA=kx2(rdrdθ)
Since x=r in polar coordinates, we can write:
dm=kr2(rdrdθ)=kr3drdθ
Step 3: Set up the integral for the moment of inertia
The moment of inertia I about an axis through O and perpendicular to the lamina is given by:
I=∫r2dm
Substituting the expression for dm:
I=∫2π0∫a0r2(kr3)drdθ
This simplifies to:
I=k∫2π0dθ∫a0r5dr
Step 4: Evaluate the integrals
First, evaluate the angular integral:
∫2π0dθ=2π
Now evaluate the radial integral:
∫a0r5dr=(r66)a0=a66
Now substituting back:
I=k⋅2π⋅a66=ka6π3
Step 5: Relate k to M
To find k in terms of M, we need the total mass M:
M=∫dm=∫2π0∫a0kr2(rdrdθ)=k∫2π0dθ∫a0r3dr
Calculating the integrals:
∫2π0dθ=2π
∫a0r3dr=(r44)a0=a44
Thus,
M=k⋅2π⋅a44=ka4π2
From this, we can solve for k:
k=2Mπa4
Step 6: Substitute k back into the moment of inertia expression
Now substituting k into the expression for I:
I=2Mπa4⋅a6π3=2Ma23
Final Result
Thus, the moment of inertia I of the lamina about an axis through O and perpendicular to the lamina is:
I=2Ma23
The mass per unit area of the lamina is given by σ=kx2, where x is the distance from the center O. The area element in polar coordinates is given by dA=rdrdθ.
The mass element dm can be expressed as:
dm=σdA=kx2dA=kx2(rdrdθ)
Since x=r in polar coordinates, we can write:
dm=kr2(rdrdθ)=kr3drdθ
The moment of inertia I about an axis through O and perpendicular to the lamina is given by:
I=∫r2dm
Substituting the expression for dm:
I=∫2π0∫a0r2(kr3)drdθ
This simplifies to:
I=k∫2π0dθ∫a0r5dr
First, evaluate the angular integral:
∫2π0dθ=2π
Now evaluate the radial integral:
∫a0r5dr=(r66)a0=a66
Now substituting back:
I=k⋅2π⋅a66=ka6π3
To find k in terms of M, we need the total mass M:
M=∫dm=∫2π0∫a0kr2(rdrdθ)=k∫2π0dθ∫a0r3dr
Calculating the integrals:
∫2π0dθ=2π
∫a0r3dr=(r44)a0=a44
Thus,
M=k⋅2π⋅a44=ka4π2
From this, we can solve for k:
k=2Mπa4
Now substituting k into the expression for I:
I=2Mπa4⋅a6π3=2Ma23
Thus, the moment of inertia I of the lamina about an axis through O and perpendicular to the lamina is:
I=2Ma23
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Multiple Correct
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 1 Objective
Explore 30 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
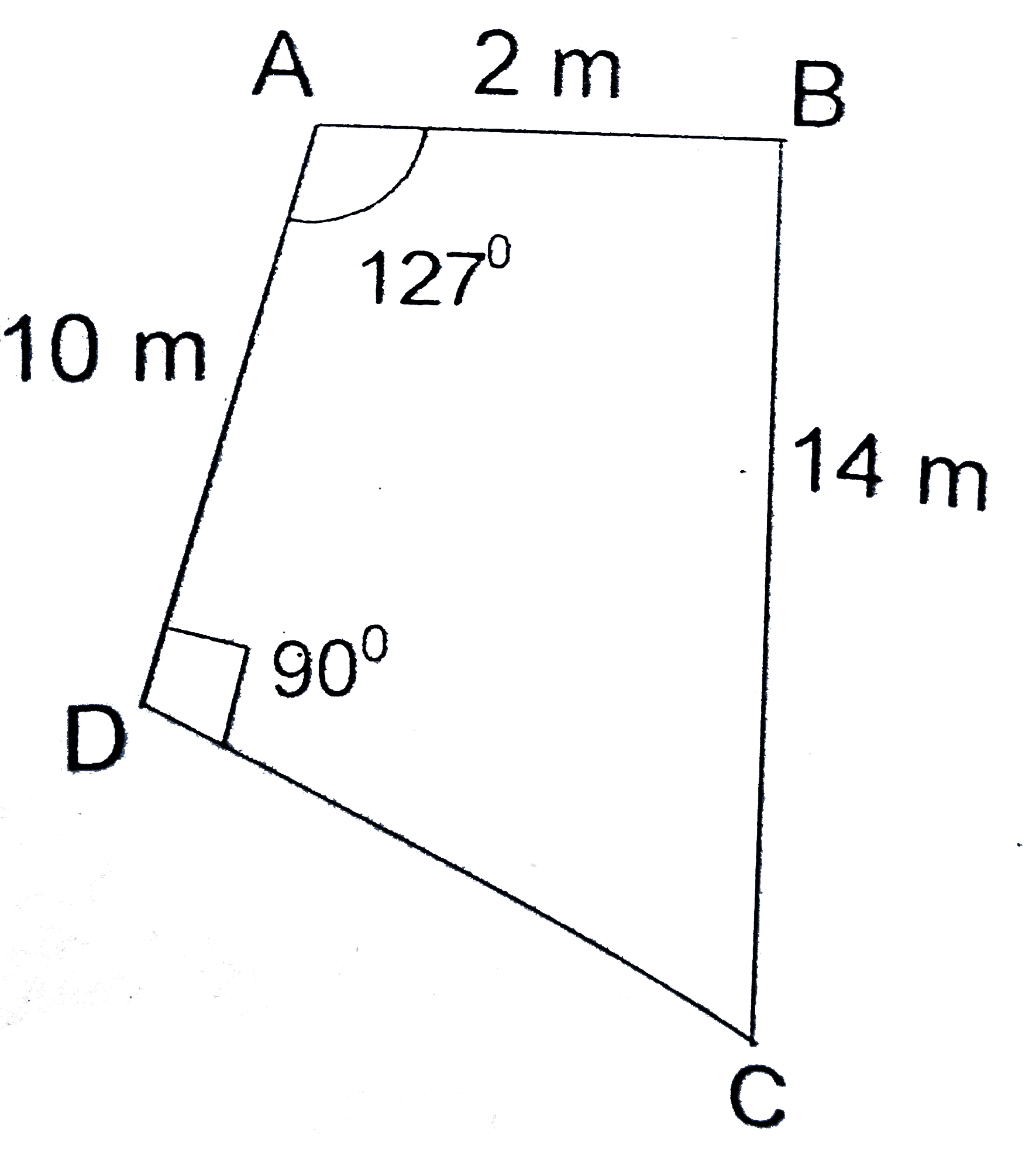
In the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calcuate the moment of inertia of the ring about an axis passing through its centre an perpendicular to its surface.
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
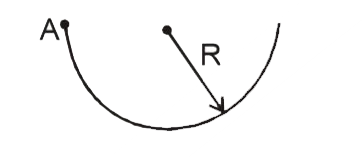
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calculate the moment of inertia of the ring about an axis passing through its center and perpendicular to its surface.
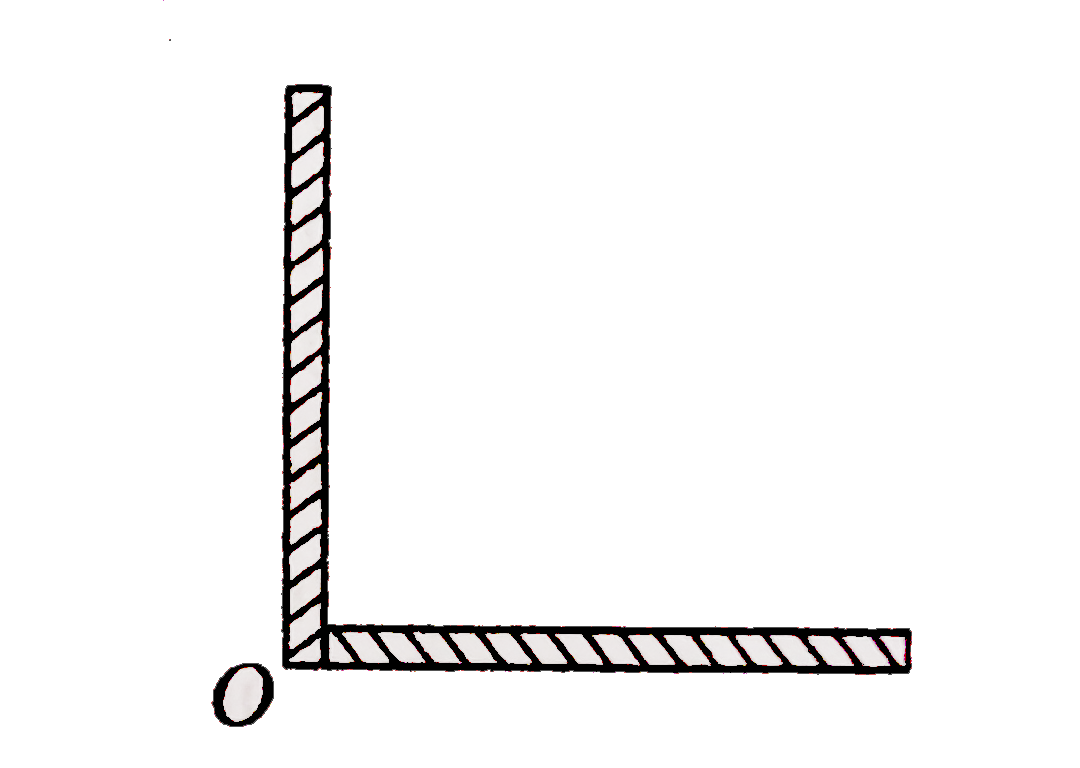
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
View SolutionA thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?

View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution

