After an head on elastic collision between two balls of equal masses, one is observed to have a speed of along the positive x-axis and the other has a speed of along the negative x-axis. What are the original velocities of the balls?
The correct Answer is:A, B, C
To solve the problem of finding the original velocities of two balls after a head-on elastic collision, we can follow these steps:
Step 1: Define the Variables
Let:
- V1 = initial velocity of ball 1 (before collision)
- V2 = initial velocity of ball 2 (before collision)
- V′1=3m/s (final velocity of ball 1 after collision, positive x-direction)
- V′2=−2m/s (final velocity of ball 2 after collision, negative x-direction)
Step 2: Apply the Conservation of Momentum
Since no external forces are acting on the system, the total momentum before the collision is equal to the total momentum after the collision.
The equation for conservation of momentum is:
mV1+mV2=mV′1+mV′2
Since the masses are equal, we can cancel m from the equation:
V1+V2=V′1+V′2
Substituting the known final velocities:
V1+V2=3+(−2)
V1+V2=1(Equation 1)
Step 3: Apply the Conservation of Kinetic Energy
For an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
The equation for conservation of kinetic energy is:
12mV21+12mV22=12m(V′21+V′22)
Again, cancel 12m:
V21+V22=V′21+V′22
Substituting the known final velocities:
V21+V22=32+(−2)2
V21+V22=9+4
V21+V22=13(Equation 2)
Step 4: Solve the Equations
Now we have two equations:
1. V1+V2=1 (Equation 1)
2. V21+V22=13 (Equation 2)
From Equation 1, we can express V2 in terms of V1:
V2=1−V1
Substituting V2 in Equation 2:
V21+(1−V1)2=13
Expanding the equation:
V21+(1−2V1+V21)=13
2V21−2V1+1=13
2V21−2V1−12=0
Dividing the entire equation by 2:
V21−V1−6=0
Step 5: Factor the Quadratic Equation
Factoring the quadratic:
(V1−3)(V1+2)=0
This gives us:
V1=3orV1=−2
Step 6: Find Corresponding V2
Using V1+V2=1:
1. If V1=3:
V2=1−3=−2
2. If V1=−2:
V2=1−(−2)=3
Conclusion
The original velocities of the balls are:
- Ball 1: V1=−2m/s (moving in the negative x-direction)
- Ball 2: V2=3m/s (moving in the positive x-direction)
Let:
- V1 = initial velocity of ball 1 (before collision)
- V2 = initial velocity of ball 2 (before collision)
- V′1=3m/s (final velocity of ball 1 after collision, positive x-direction)
- V′2=−2m/s (final velocity of ball 2 after collision, negative x-direction)
Since no external forces are acting on the system, the total momentum before the collision is equal to the total momentum after the collision.
mV1+mV2=mV′1+mV′2
Since the masses are equal, we can cancel m from the equation:
V1+V2=V′1+V′2
Substituting the known final velocities:
V1+V2=3+(−2)
V1+V2=1(Equation 1)
For an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
12mV21+12mV22=12m(V′21+V′22)
Again, cancel 12m:
V21+V22=V′21+V′22
Substituting the known final velocities:
V21+V22=32+(−2)2
V21+V22=9+4
V21+V22=13(Equation 2)
Now we have two equations:
1. V1+V2=1 (Equation 1)
2. V21+V22=13 (Equation 2)
V2=1−V1
V21+(1−V1)2=13
Expanding the equation:
V21+(1−2V1+V21)=13
2V21−2V1+1=13
2V21−2V1−12=0
Dividing the entire equation by 2:
V21−V1−6=0
Factoring the quadratic:
(V1−3)(V1+2)=0
This gives us:
V1=3orV1=−2
Using V1+V2=1:
1. If V1=3:
V2=1−3=−2
2. If V1=−2:
V2=1−(−2)=3
The original velocities of the balls are:
- Ball 1: V1=−2m/s (moving in the negative x-direction)
- Ball 2: V2=3m/s (moving in the positive x-direction)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.5
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two balls of equal mass have a head-on collision with speed 6m/s. If the coefficient of restitution is 13, find the speed of each ball after impact in m/s
View SolutionA gun is mounted on a trolley which can move uniformly with speed vm/s along the x-axis. Two shots are find from the origin with the gun making an angle 30∘ with the horizontal such that in the first case the trolley is moving along the positive x-axis and in the second case moving along the negative x- axis. The respective range of the projectile is 250m and 200m, along the x−axis. Find the velocity of the trolley in m/s. (Assume height of the trolley to be negligible)(given g=10m/s2).
View SolutionConsider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
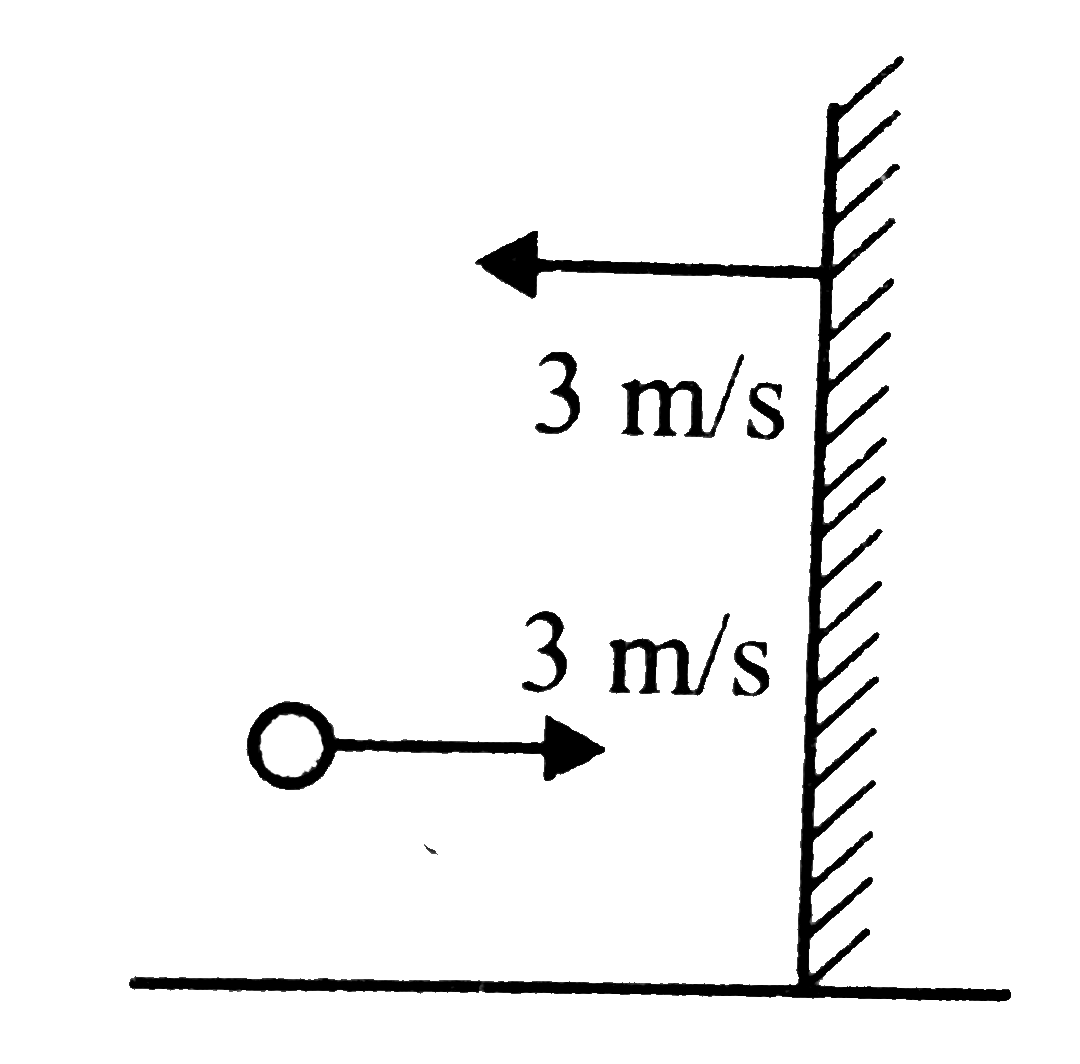
View SolutionA ball of mass 0.2 kg travelling in a straight line with a speed of m/s along negative x- axis id deflected by a bat 15m/s along negative x - axis is deflected by a bat at an angle of 30∘ If the speed of the ball after deflection is 10m/s, find the impulse on the ball.
View SolutionTwo balls roll towards each other. The red ball has a mass kg 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2m/s. after the head-on collision, the red ball continues forward with a speed of 2m/s. find the speed of the green ball after the collision. was the collision elastic?
View SolutionTwo bodies of masses m and 2m are moving along positive x and y axes respectively with equal speed 4ms−1. They collide at origin and stick together. The final velocity of combined mass is
View SolutionA particle moves along x-axis with speed 6m/s for the first half distance of a journey and the second half distance with a speed 3m/s. The average speed in the total journey is
View SolutionA ball is thrown from the origin in the x-y plane with velocity 28.28m/s at an angle of 45∘ with x-axis.At the same instant a trolley also starts moving with uniform velocity of 10m/s along the positive x-axis . Initially , the trolley is located at 38m from the origin. Determine the time at which the ball hits the trolley.
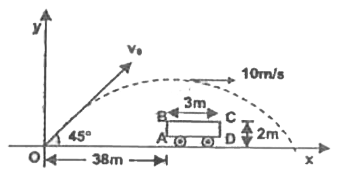
View SolutionBlocks A and B are moving towards each other along the x axis. A has mass of 2.0 kg and a velocity of 10 m/s (in the positive x direction), B has a mass of 3.0 kg and a velocity of –5 m/s (in the negative x direction). They suffer an elastic collision and move off along the x axis. After the collision, the velocities of A and B, respectively, are:
View Solution
