A ball falls vertically on an inclined plane of inclination α with speed v0 and makes a perfectly elastic collision. What is angle of velocity vector with horizontal after collision.
The correct Answer is:A, B
To solve the problem of finding the angle of the velocity vector with the horizontal after a perfectly elastic collision of a ball falling vertically onto an inclined plane, we can follow these steps:
1. Identify the Initial Conditions:
- The ball falls vertically with an initial speed v0.
- The inclined plane makes an angle α with the horizontal.
2. Resolve the Initial Velocity:
- The initial velocity v0 can be resolved into two components relative to the inclined plane:
- Perpendicular to the inclined plane: v0⊥=v0cos(α)
- Parallel to the inclined plane: v0∥=v0sin(α)
3. Understand the Collision:
- Since the collision is perfectly elastic, the component of velocity perpendicular to the inclined plane will change direction but maintain its magnitude.
- The parallel component of velocity will remain unchanged.
4. Determine the Components After Collision:
- After the collision, the new velocity components will be:
- Perpendicular to the inclined plane: v1⊥=−v0cos(α) (changes direction)
- Parallel to the inclined plane: v1∥=v0sin(α) (remains the same)
5. Combine the Velocity Components:
- The final velocity vector →Vf can be expressed as:
→Vf=v1∥^p+v1⊥^n
- Substituting the values:
→Vf=v0sin(α)^p−v0cos(α)^n
6. Convert to Cartesian Coordinates:
- The components can be expressed in terms of the horizontal (x) and vertical (y) directions:
- Horizontal component: Vfx=v0sin(α)
- Vertical component: Vfy=−v0cos(α)
7. Calculate the Angle with the Horizontal:
- The angle θ with the horizontal can be found using the tangent function:
tan(θ)=VfyVfx=−v0cos(α)v0sin(α)=−cot(α)
- Therefore, the angle θ can be expressed as:
θ=tan−1(−cot(α))
8. Final Result:
- The angle of the velocity vector with the horizontal after the collision is:
θ=tan−1(−cot(α))
- The ball falls vertically with an initial speed v0.
- The inclined plane makes an angle α with the horizontal.
- The initial velocity v0 can be resolved into two components relative to the inclined plane:
- Perpendicular to the inclined plane: v0⊥=v0cos(α)
- Parallel to the inclined plane: v0∥=v0sin(α)
- Since the collision is perfectly elastic, the component of velocity perpendicular to the inclined plane will change direction but maintain its magnitude.
- The parallel component of velocity will remain unchanged.
- After the collision, the new velocity components will be:
- Perpendicular to the inclined plane: v1⊥=−v0cos(α) (changes direction)
- Parallel to the inclined plane: v1∥=v0sin(α) (remains the same)
- The final velocity vector →Vf can be expressed as:
→Vf=v1∥^p+v1⊥^n
- Substituting the values:
→Vf=v0sin(α)^p−v0cos(α)^n
- The components can be expressed in terms of the horizontal (x) and vertical (y) directions:
- Horizontal component: Vfx=v0sin(α)
- Vertical component: Vfy=−v0cos(α)
- The angle θ with the horizontal can be found using the tangent function:
tan(θ)=VfyVfx=−v0cos(α)v0sin(α)=−cot(α)
- Therefore, the angle θ can be expressed as:
θ=tan−1(−cot(α))
- The angle of the velocity vector with the horizontal after the collision is:
θ=tan−1(−cot(α))
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion And Reason
Explore 15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Objective
Explore 42 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.5
Explore 4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A ball falls vertically on an inclined plane of inclination α with speed v0 and makes a perfectly elastic collision. What is angle of velocity vector with horizontal after collision.
View Solution
Derive final velocities V1andV2 after perfectly elastic collision.
View SolutionA ball falls from height h over an inclined plane of inclination 30°C as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_E05_227_Q001.png)
View SolutionA ball falls from height h over an inclined plane of inclination 30∘ as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_224_Q01.png)
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
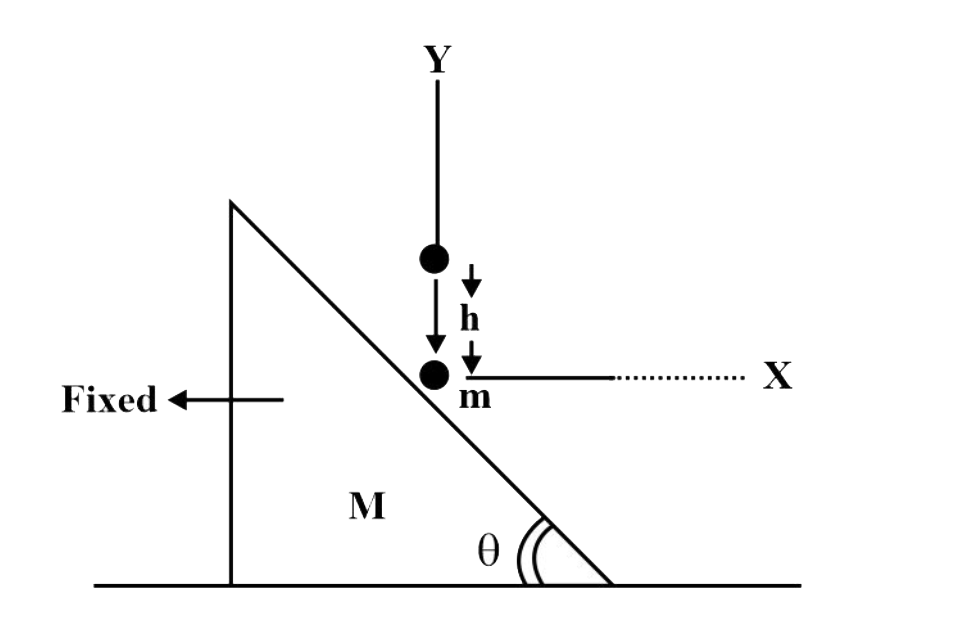
View SolutionA ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
View SolutionA ball is projected perpendicularly from an inclined plane of angle θ, with speed 'u' as shown. The time after which the projectile is making angle 45∘ with the inclined plane is :

View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View SolutionTwo identical balls are rolling without slipping on a horizontal plane as shwon in figure. They undergo a perfect elastic collision. Just after collision, the velocity of image of the bottom point of A with respect to the plane mirros is x V, then x=

View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is :
View Solution