In one dimensional elastic collison of equla masses, the velocities are interchanged. Can velocities ina one dimensional collision be interchanged if the masses are not equal?
To determine whether the velocities can be interchanged in a one-dimensional elastic collision when the masses are not equal, we can analyze the situation using the principles of conservation of momentum and conservation of kinetic energy.
Step 1: Define the Problem
We have two masses, m1 and m2, with initial velocities u1 and u2 respectively. We want to find out if, after an elastic collision, the final velocities v1 and v2 can be equal to u2 and u1 respectively (i.e., if the velocities can be interchanged).
Hint: Start by recalling the definitions of elastic collision and the conservation laws.
Step 2: Apply Conservation of Momentum
The total momentum before the collision must equal the total momentum after the collision:
m1u1+m2u2=m1v1+m2v2
Hint: Write down the equation for momentum conservation and identify the variables involved.
Step 3: Apply Conservation of Kinetic Energy
In an elastic collision, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
12m1u21+12m2u22=12m1v21+12m2v22
Hint: Remember that kinetic energy is a function of the square of velocity, which will play a role in the equations.
Step 4: Derive the Final Velocities
From the conservation laws, we can derive the final velocities v1 and v2:
v1=(m1−m2)(m1+m2)u1+2m2(m1+m2)u2
v2=2m1(m1+m2)u1+(m2−m1)(m1+m2)u2
Hint: Substitute m1 and m2 into the equations and simplify to see if v1 can equal u2 and v2 can equal u1.
Step 5: Analyze the Case of Equal Masses
If m1=m2, the equations simplify significantly:
v1=u2
v2=u1
This shows that the velocities can be interchanged when the masses are equal.
Hint: Consider what happens to the equations when the masses are not equal.
Step 6: Conclusion for Unequal Masses
When m1 and m2 are not equal, the derived equations for v1 and v2 do not simplify to the case where v1=u2 and v2=u1. Therefore, the velocities cannot be interchanged.
Final Answer: No, the velocities in a one-dimensional elastic collision cannot be interchanged if the masses are not equal.
We have two masses, m1 and m2, with initial velocities u1 and u2 respectively. We want to find out if, after an elastic collision, the final velocities v1 and v2 can be equal to u2 and u1 respectively (i.e., if the velocities can be interchanged).
The total momentum before the collision must equal the total momentum after the collision:
In an elastic collision, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
From the conservation laws, we can derive the final velocities v1 and v2:
If m1=m2, the equations simplify significantly:
v2=u1
When m1 and m2 are not equal, the derived equations for v1 and v2 do not simplify to the case where v1=u2 and v2=u1. Therefore, the velocities cannot be interchanged.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.5
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
In one dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in one dimensional collision be interchanged if the masses are not equal?
View SolutionIn one dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in one dimensional collision be interchanged if the masses are not equal?
View Solution
Knowledge Check
Consider the following statements A and B. Identify the correct choice in the given answers
A. In a one dimensional perfectly elastic collision between two moving bodies of equal masses the bodies merely exchange their velocities after collision.
B. If a lighter body at rest suffers perfectly elastic collision with a very heavy body moving with a certain velocity, then after collision both travel with same velocity.AA and B are correctBBoth A and B are wrongCA is correct, B is wrongDA is wrong, B is correctIn an elastic one dimensional collision between two particles the relative veloctiy of approach before collision is
Agreater than the relative velocity of separation after collisionBless than the relative velocity of separation after collisionCequal to the relative velocity of separation after collisionDless than the relative velocity of separation if the incoming particle is heavier than the target particle
In a head on elastic collision of two bodies of equal masses
View SolutionDiscuss elastic collision in one dimension. Obtain expressions for velocities of the two bodies after such a collision.
View SolutionWhich of the following statements can be possible cases in one//two dimensional motion ?
View SolutionIn figure, determine the character of the collision. The masses of the blocks, and the velocities before and after are given. The collision is
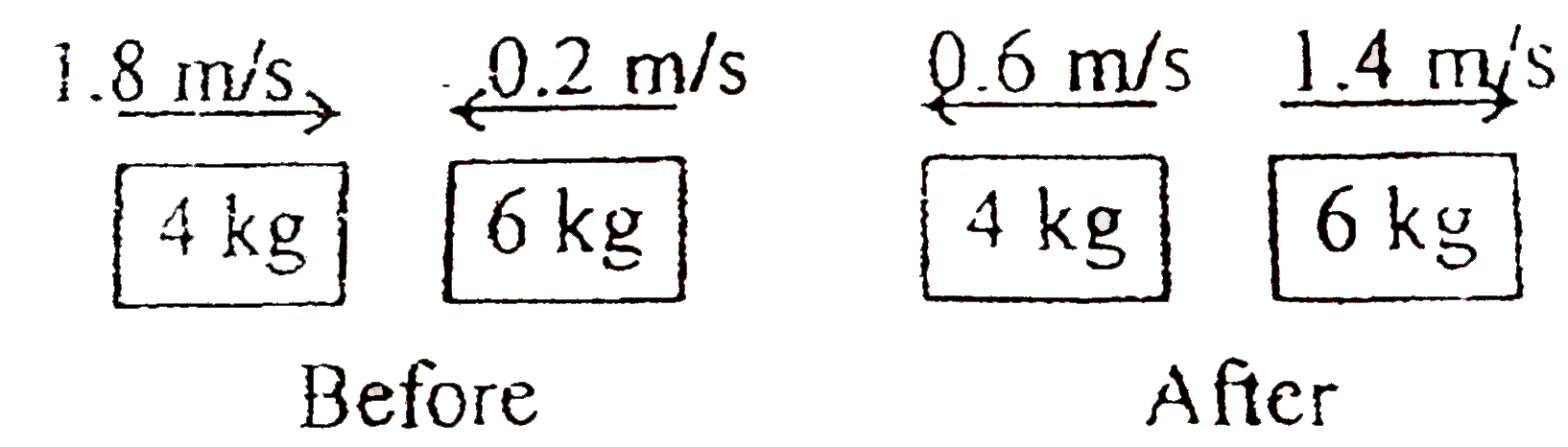
View SolutionFrom study of elastic collision we understand that if two colliding particles have equal masses they interchange their velocities and energy transfer is maximum if they have equal masses and one is at rest w... other. This principle can be easily used in nuclear reactor to select a moderator. If m1=m2=m and m2 at rest then m1 will stop after colliding with m2 and m2 will move with velocity of m1. In case of nuclear reactor we used a moderator such that neutrons can be slowed down. With above reference answer the following questions
Which is correct statement
View SolutionSTATEMENT-1 : When a projectile explodes in mid air the centre of mass follows circular path after explosion.
STATEMENT-2 : In an elastic collision velocities can't be interchanged it colliding bodies have different masses.
STATEMENT-3 : During a perfectly elastic collision the kinetic energy of the system remains constant.
View Solution
