Two particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
To solve the problem, we need to find the displacement of the center of mass of the two particles after 1 second.
1. Identify the masses and initial positions:
- Mass of particle 1, m1=1kg
- Mass of particle 2, m2=2kg
- Initial distance between them = 10 m
2. Determine the initial positions of the particles:
- Let the initial position of particle 1 be at x1=0m.
- Therefore, the initial position of particle 2 will be x2=10m.
3. Determine the velocities of the particles:
- Velocity of particle 1, v1=2m/s (moving towards particle 2)
- Velocity of particle 2, v2=−1m/s (moving towards particle 1, hence negative)
4. Calculate the displacement of each particle after 1 second:
- Displacement of particle 1 after 1 second:
s1=v1⋅t=2m/s⋅1s=2m
- Displacement of particle 2 after 1 second:
s2=v2⋅t=−1m/s⋅1s=−1m
5. Determine the new positions of the particles:
- New position of particle 1:
x′1=x1+s1=0+2=2m
- New position of particle 2:
x′2=x2+s2=10−1=9m
6. Calculate the center of mass (CM) position before and after the displacement:
- Initial center of mass position xCM:
xCM=m1x1+m2x2m1+m2=1⋅0+2⋅101+2=203m
- New center of mass position x′CM:
x′CM=m1x′1+m2x′2m1+m2=1⋅2+2⋅91+2=203m
7. Calculate the displacement of the center of mass:
- Displacement of center of mass:
ΔxCM=x′CM−xCM=203−203=0m
Final Answer:
The displacement of the center of mass at t=1s is 0m.
- Mass of particle 1, m1=1kg
- Mass of particle 2, m2=2kg
- Initial distance between them = 10 m
- Let the initial position of particle 1 be at x1=0m.
- Therefore, the initial position of particle 2 will be x2=10m.
- Velocity of particle 1, v1=2m/s (moving towards particle 2)
- Velocity of particle 2, v2=−1m/s (moving towards particle 1, hence negative)
- Displacement of particle 1 after 1 second:
s1=v1⋅t=2m/s⋅1s=2m
- Displacement of particle 2 after 1 second:
s2=v2⋅t=−1m/s⋅1s=−1m
- New position of particle 1:
x′1=x1+s1=0+2=2m
- New position of particle 2:
x′2=x2+s2=10−1=9m
- Initial center of mass position xCM:
xCM=m1x1+m2x2m1+m2=1⋅0+2⋅101+2=203m
- New center of mass position x′CM:
x′CM=m1x′1+m2x′2m1+m2=1⋅2+2⋅91+2=203m
- Displacement of center of mass:
ΔxCM=x′CM−xCM=203−203=0m
The displacement of the center of mass at t=1s is 0m.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.3
Explore 7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.4
Explore 4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.1
Explore 13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
Two bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
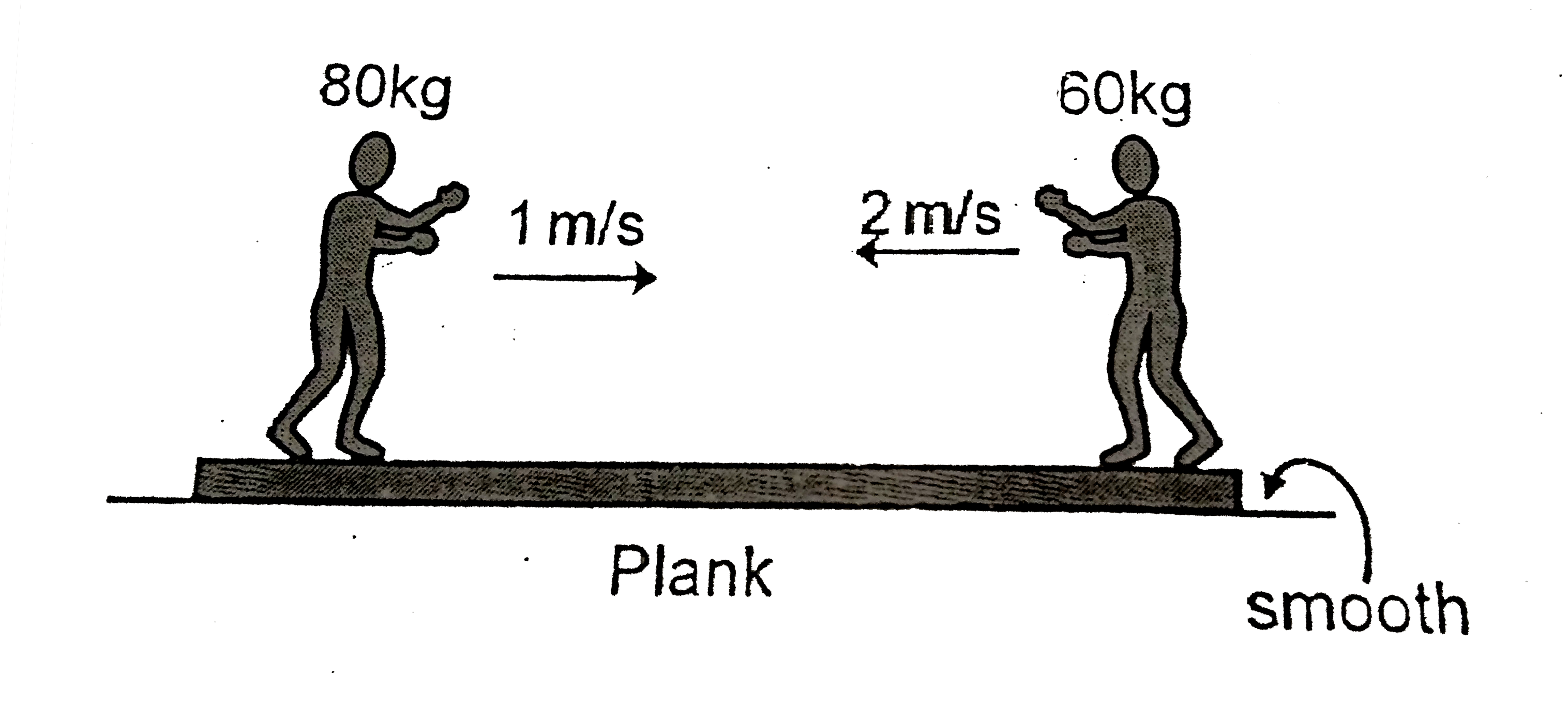
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 2kg and 4kg are approaching towards each other with ccelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal suface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View Solution10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View Solution