Two particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
To find the speed of the center of mass of the system consisting of two particles, we can follow these steps:
1. Identify the Masses and Velocities:
- Let the mass of the first particle m1=1kg and its velocity v1=2m/s.
- Let the mass of the second particle m2=2kg and its velocity v2=4m/s.
2. Use the Formula for the Velocity of the Center of Mass:
The formula for the velocity of the center of mass Vcm for a system of particles is given by:
Vcm=m1v1+m2v2m1+m2
3. Substitute the Values into the Formula:
Substitute the known values into the formula:
Vcm=(1kg×2m/s)+(2kg×4m/s)1kg+2kg
4. Calculate the Numerator:
- Calculate m1v1=1×2=2kg m/s
- Calculate m2v2=2×4=8kg m/s
- Therefore, the total momentum is 2+8=10kg m/s.
5. Calculate the Denominator:
- Calculate the total mass: m1+m2=1+2=3kg.
6. Calculate the Velocity of the Center of Mass:
Substitute the values back into the formula:
Vcm=10kg m/s3kg=103m/s≈3.33m/s
Final Answer:
The speed of the center of mass of the system is approximately 3.33m/s.
---
- Let the mass of the first particle m1=1kg and its velocity v1=2m/s.
- Let the mass of the second particle m2=2kg and its velocity v2=4m/s.
The formula for the velocity of the center of mass Vcm for a system of particles is given by:
Vcm=m1v1+m2v2m1+m2
Substitute the known values into the formula:
Vcm=(1kg×2m/s)+(2kg×4m/s)1kg+2kg
- Calculate m1v1=1×2=2kg m/s
- Calculate m2v2=2×4=8kg m/s
- Therefore, the total momentum is 2+8=10kg m/s.
- Calculate the total mass: m1+m2=1+2=3kg.
Substitute the values back into the formula:
Vcm=10kg m/s3kg=103m/s≈3.33m/s
The speed of the center of mass of the system is approximately 3.33m/s.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then
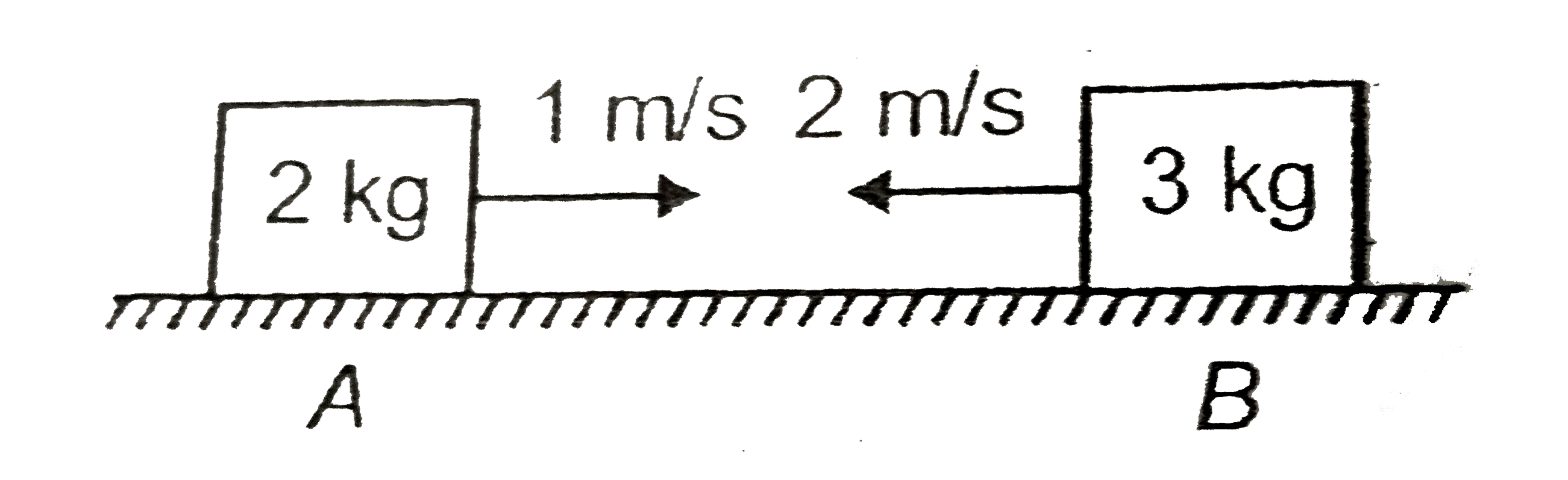
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
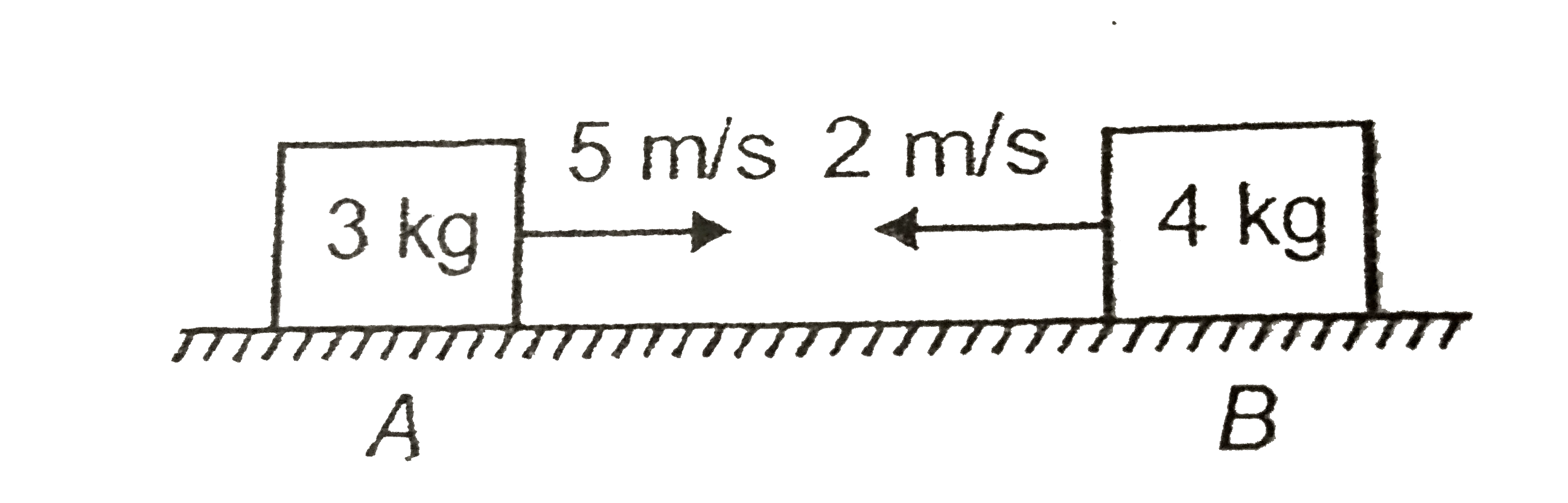
Velocity of A after collision
View Solution
