A projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
u2(√21)2g
3u24g
u22β
(√21)u28g
The correct Answer is:D
To solve the problem of finding the range of a projectile projected at an angle of 60∘ to the horizontal from the foot of an inclined plane, we can follow these steps:
Step 1: Resolve the Initial Velocity
The initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component:
ux=ucos60∘=u2
- Vertical component:
uy=usin60∘=√3u2
Step 2: Understand the Projectile Motion
When the projectile hits the inclined plane horizontally, it means that at the point of impact, the vertical component of the velocity Vy=0. This occurs at the maximum height of the projectile.
Step 3: Calculate the Maximum Height
The maximum height H reached by the projectile can be calculated using the formula:
H=u2y2g=(√3u2)22g=3u28g
Step 4: Calculate the Horizontal Range on the Inclined Plane
The horizontal range R on the inclined plane can be calculated using the formula for the range of a projectile:
R=u2sin2θg
For our case, θ=60∘:
R=u2sin120∘g=u2⋅√32g=√3u22g
Since we are interested in the range on the inclined plane, we need to find half of this range:
R2=√3u24g
Step 5: Use Pythagorean Theorem
Let’s denote the height H and the horizontal distance D as:
- AB=H=3u28g
- BC=R2=√3u24g
Now, we can find the length of the incline AC using the Pythagorean theorem:
AC=√AB2+BC2
Substituting the values:
AC=
⎷(3u28g)2+(√3u24g)2
Calculating:
=√9u464g2+3u416g2=√9u464g2+12u464g2=√21u464g2=u2√218g
Final Answer
Thus, the range on the inclined plane is:
Range on inclined plane=u2√218g
---
The initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component:
ux=ucos60∘=u2
- Vertical component:
uy=usin60∘=√3u2
When the projectile hits the inclined plane horizontally, it means that at the point of impact, the vertical component of the velocity Vy=0. This occurs at the maximum height of the projectile.
The maximum height H reached by the projectile can be calculated using the formula:
H=u2y2g=(√3u2)22g=3u28g
The horizontal range R on the inclined plane can be calculated using the formula for the range of a projectile:
R=u2sin2θg
For our case, θ=60∘:
R=u2sin120∘g=u2⋅√32g=√3u22g
Since we are interested in the range on the inclined plane, we need to find half of this range:
R2=√3u24g
Let’s denote the height H and the horizontal distance D as:
- AB=H=3u28g
- BC=R2=√3u24g
AC=√AB2+BC2
Substituting the values:
AC=
⎷(3u28g)2+(√3u24g)2
Calculating:
=√9u464g2+3u416g2=√9u464g2+12u464g2=√21u464g2=u2√218g
Thus, the range on the inclined plane is:
Range on inclined plane=u2√218g
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Subjective
21 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View SolutionA projectile is launched with a speed of an angle 60∘ with the horizontal from a sloping surface of inclination 30∘. The range R is: (g=10m/s2)
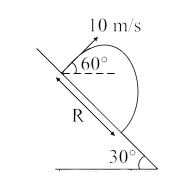
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionFour projectiles are projected with the same speed at angles 20∘,35∘,60∘and75∘
with the horizontal. The range will be the maximum for the projectile whose angle of projection is
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionAn inclined plane makes an angle of 60∘ with horizontal. A disc rolling down this inclined plane without slipping has a linear acceleration equal to
View Solution
