At a height of 45 m from ground velocity of a projectile is,
v=(30ˆi+40ˆj)m/s
Find initial velocity, time of flight, maximum height and horizontal range of this projectile. Here ˆi andˆj are the unit vectors in horizontal and vertical directions.
The correct Answer is:A, B, C, D
To solve the problem, we will follow these steps:
Step 1: Identify Given Information
- The height (h) at which the velocity is given: h=45m
- The velocity at this height:
v=30^i+40^jm/s
- Horizontal component (vx): 30m/s
- Vertical component (vy): 40m/s
Step 2: Find the Initial Vertical Velocity (uy)
Using the equation of motion in the vertical direction:
v2y=u2y+2gh
Rearranging gives:
u2y=v2y−2gh
Substituting the known values (g=10m/s2):
u2y=402−2⋅10⋅45
Calculating:
u2y=1600−900=700
Thus,
uy=√700=10√7≈26.46m/s
Step 3: Find the Initial Horizontal Velocity (ux)
Since the horizontal component of velocity remains constant:
ux=vx=30m/s
Step 4: Calculate the Magnitude of the Initial Velocity (u)
Using Pythagoras' theorem:
u=√u2x+u2y
Substituting the values:
u=√302+(10√7)2=√900+700=√1600=40m/s
Step 5: Calculate the Angle of Projection (θ)
Using the tangent function:
tanθ=uyux=10√730=√73
Thus,
θ=tan−1(√73)
Step 6: Calculate Time of Flight (T)
Using the formula for time of flight:
T=2uyg
Substituting the values:
T=2⋅10√710=2√7≈5.29s
Step 7: Calculate Maximum Height (H)
Using the formula for maximum height:
H=u2y2g
Substituting the values:
H=(10√7)22⋅10=70020=35m
Step 8: Calculate Horizontal Range (R)
Using the formula for horizontal range:
R=ux⋅T
Substituting the values:
R=30⋅2√7≈30⋅5.29≈158.7m
Summary of Results
- Initial Velocity (u): 40m/s
- Time of Flight (T): 5.29s
- Maximum Height (H): 35m
- Horizontal Range (R): 158.7m
- The height (h) at which the velocity is given: h=45m
- The velocity at this height:
v=30^i+40^jm/s
- Horizontal component (vx): 30m/s
- Vertical component (vy): 40m/s
Using the equation of motion in the vertical direction:
v2y=u2y+2gh
Rearranging gives:
u2y=v2y−2gh
Substituting the known values (g=10m/s2):
u2y=402−2⋅10⋅45
Calculating:
u2y=1600−900=700
Thus,
uy=√700=10√7≈26.46m/s
Since the horizontal component of velocity remains constant:
ux=vx=30m/s
Using Pythagoras' theorem:
u=√u2x+u2y
Substituting the values:
u=√302+(10√7)2=√900+700=√1600=40m/s
Using the tangent function:
tanθ=uyux=10√730=√73
Thus,
θ=tan−1(√73)
Using the formula for time of flight:
T=2uyg
Substituting the values:
T=2⋅10√710=2√7≈5.29s
Using the formula for maximum height:
H=u2y2g
Substituting the values:
H=(10√7)22⋅10=70020=35m
Using the formula for horizontal range:
R=ux⋅T
Substituting the values:
R=30⋅2√7≈30⋅5.29≈158.7m
- Initial Velocity (u): 40m/s
- Time of Flight (T): 5.29s
- Maximum Height (H): 35m
- Horizontal Range (R): 158.7m
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Miscellaneous Examples
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 4
1 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
At a height of 15 m from ground velocity of a projectile is v=(10ˆi+10ˆj). Here ˆj is vertically upwards and ˆi is along horizontal direction then (g = 10 ms−1)
View SolutionIf the maximum vertical height and horizontal ranges of a projectile are same, the angle of projection will be
View SolutionFind (a) time of flight , (b) Max.height (c ) Horizontal range of projectile projected with speed (v) making an angle θ with the horizontal direction from ground.
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)m/s. Its velocity (in m/s) at point B is

View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)ms. It's velocity (in m/s) at point B is -
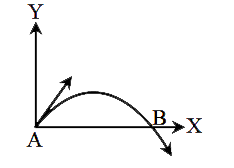
View SolutionAssertion At height 20 m from ground , velocity of a projectile is v=(20ˆi+10ˆj)ms−1. Here, ˆi is horizontal and ˆj is vertical. Then, the particle is at the same height after 4s.
Reason Maximum height of particle from ground is 40m (take, g=10ms−2)
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)ms−1. Its velocity (in ms−1) at point B is
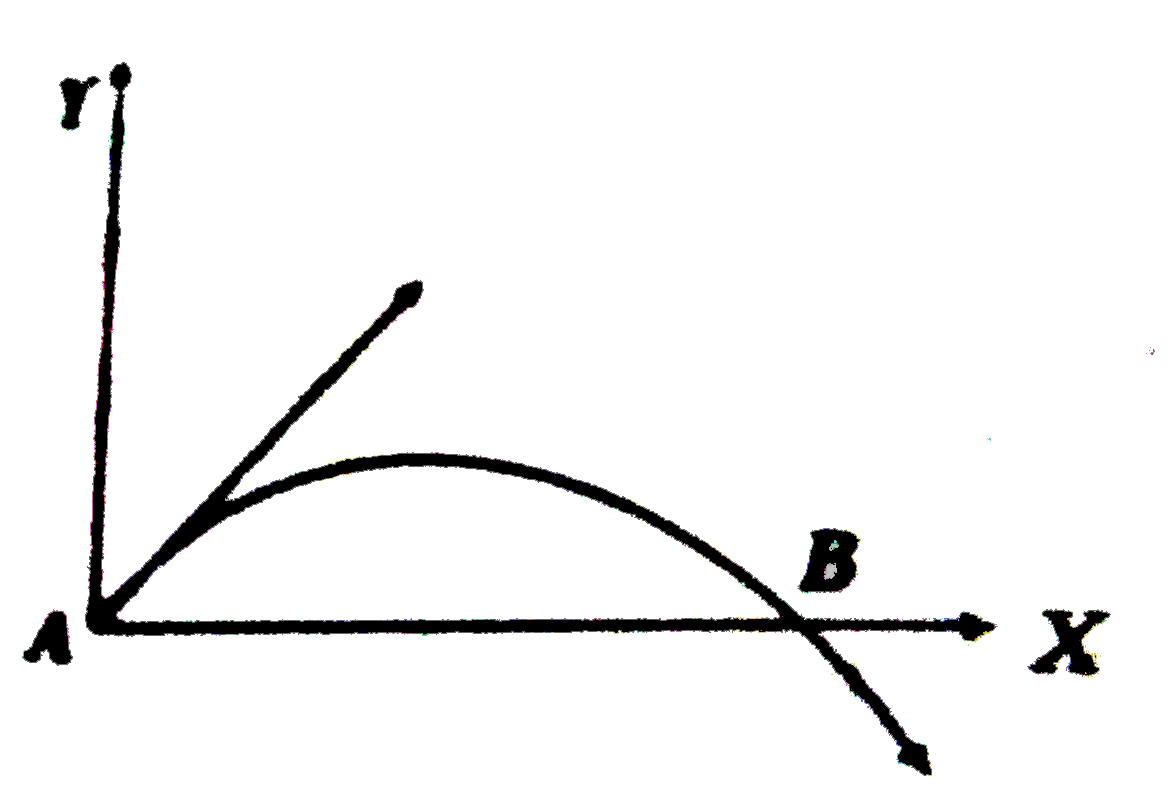
View SolutionThe maximum range of a projecitle fired with some initial velocity is found to be 1000 metre The maximum height (H) reached by this projectile is:-
View SolutionThe velocity of projection of oblique projectile is (6ˆi+8ˆj)ms−1 The horizontal range of the projectile is
View Solution
