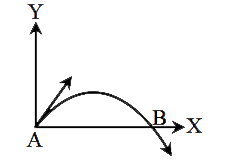
The velocity of a projectile at the initial point A is $(2 ˆ i + 3 ˆ j) \frac{m}{s} .$ It's velocity (in m/s) at point B is -

A

$- 2 ˆ i - 3 ˆ j$

B

$- 2 ˆ i + 3 ˆ j$

C

$2 ˆ i - 3 ˆ j$

D

$2 ˆ i + 3 ˆ j$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

So, $v_{f} = 2 ˆ i - 3 ˆ j$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

The velocity of a projectile at the initial point A is $(2 ˆ i + 3 ˆ j) m / s$ . Its velocity (in m/s) at point B is

View Solution
The velocity of a projectile at the initial point A is $(2 ˆ i + 3 ˆ j) m s^{- 1}$ . Its velocity (in $m s^{- 1})$ at point B is

View Solution
Velocity of a projectile at height $15 m$ from ground is $v = (20 ˆ i + 10 ˆ j) m / s$ . Here $ˆ i$ is in horizontal direction and $ˆ j$ is vertically upwards. Then
Angle of projectile with ground is
View Solution
Velocity of a projectile at height $15 m$ from ground is $v = (20 ˆ i + 10 ˆ j) m / s$ . Here $ˆ i$ is in horizontal direction and $ˆ j$ is vertically upwards. Then
Horizontal range of the ground is ………… $m$
View Solution
Velocity of a projectile at height $15 m$ from ground is $v = (20 ˆ i + 10 ˆ j) m / s$ . Here $ˆ i$ is in horizontal direction and $ˆ j$ is vertically upwards. Then
Maximum height from a ground is …….. $m$
View Solution
Velocity of a projectile at height $15 m$ from ground is $v = (20 ˆ i + 10 ˆ j) m / s$ . Here $ˆ i$ is in horizontal direction and $ˆ j$ is vertically upwards. Then
Speed with which particle is projected from ground is……… m/s
View Solution
At a height of 45 m from ground velocity of a projectile is,
$v = (30 ˆ i + 40 ˆ j) m / s$
Find initial velocity, time of flight, maximum height and horizontal range of this projectile. Here $ˆ i$ and $ˆ j$ are the unit vectors in horizontal and vertical directions.
View Solution
Find the velocity of a projectile at the highest point, if it is projected with a speed $15 m s^{- 1}$ in the direction $45^{\circ}$ above horizontla. (take g = $10 m s^{- 2})$
View Solution
The velocity of an object is given by $\to v = (6 t^{3} ˆ i + t^{2} ˆ j) m / s$ . Find the acceleration at t = 2s.
View Solution
The velocity of an object is given by $\to v = (6 t^{3} ˆ i + t^{2} ˆ j) m / s)$ . Find the acceleration at t = 2s.
View Solution

The velocity of a projectile at the initial point A is (2ˆi+3ˆj)ms. It's velocity (in m/s) at point B is -

The correct Answer is:C

So, vf=2ˆi−3ˆj

Similar Questions

Recommended Questions

The velocity of a projectile at the initial point A is $(2 ˆ i + 3 ˆ j) \frac{m}{s} .$ It's velocity (in m/s) at point B is -

So, $v_{f} = 2 ˆ i - 3 ˆ j$