In the figure shown, find.
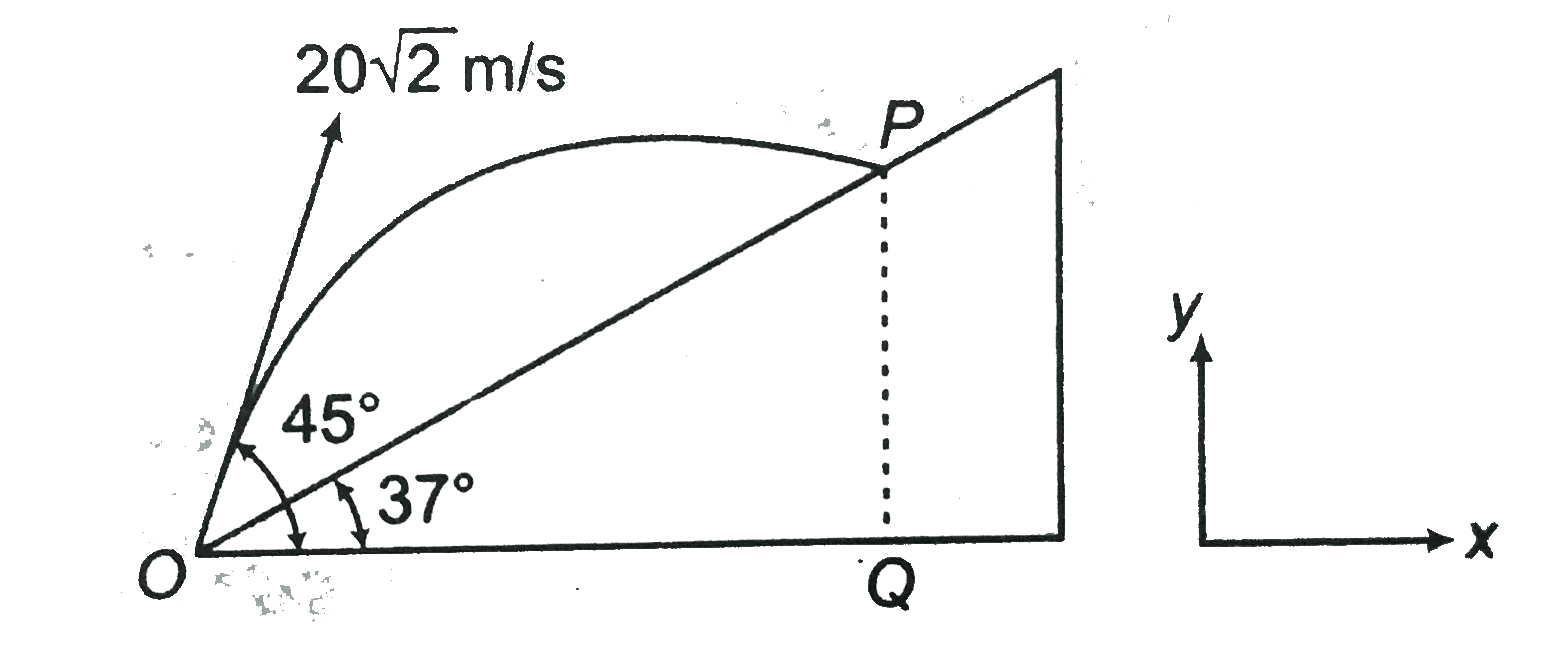
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
The correct Answer is:A, B
(a) Horizontal component of initial velocity,
ux=20(√2)cos45∘=20m/s
Vertical component of initial velocity
uy=20(√2)sin45∘=20m/s
Let the particle strikes at P after time t, then
horizontal displacement OQ=uxt=20t
In vertical displacement, uyt or 20t is upwards and 12gt2 or 5t2 is downwards. But net
displacement is upwards, therefore 20 t should be greater than 5t2 and
QP=20t−5t2
In ΔOPQ,
tan37∘=(QPOQ)
or, 34=(20t−5t220t)
Solving this equation, we get
t=1s
(b) Range OP=OQsec37∘
=(20t)(54)
Substituting t = 1s, we have
OP = 25m .
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Miscellaneous Examples
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 4
1 Video
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Knowledge Check
The time of flight of projectile on an upward inclined plane depends upon.
Aangle of projectionBangle of inclination of the planeCair resistanceDa and b both
In the figure shown

find the range R.
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
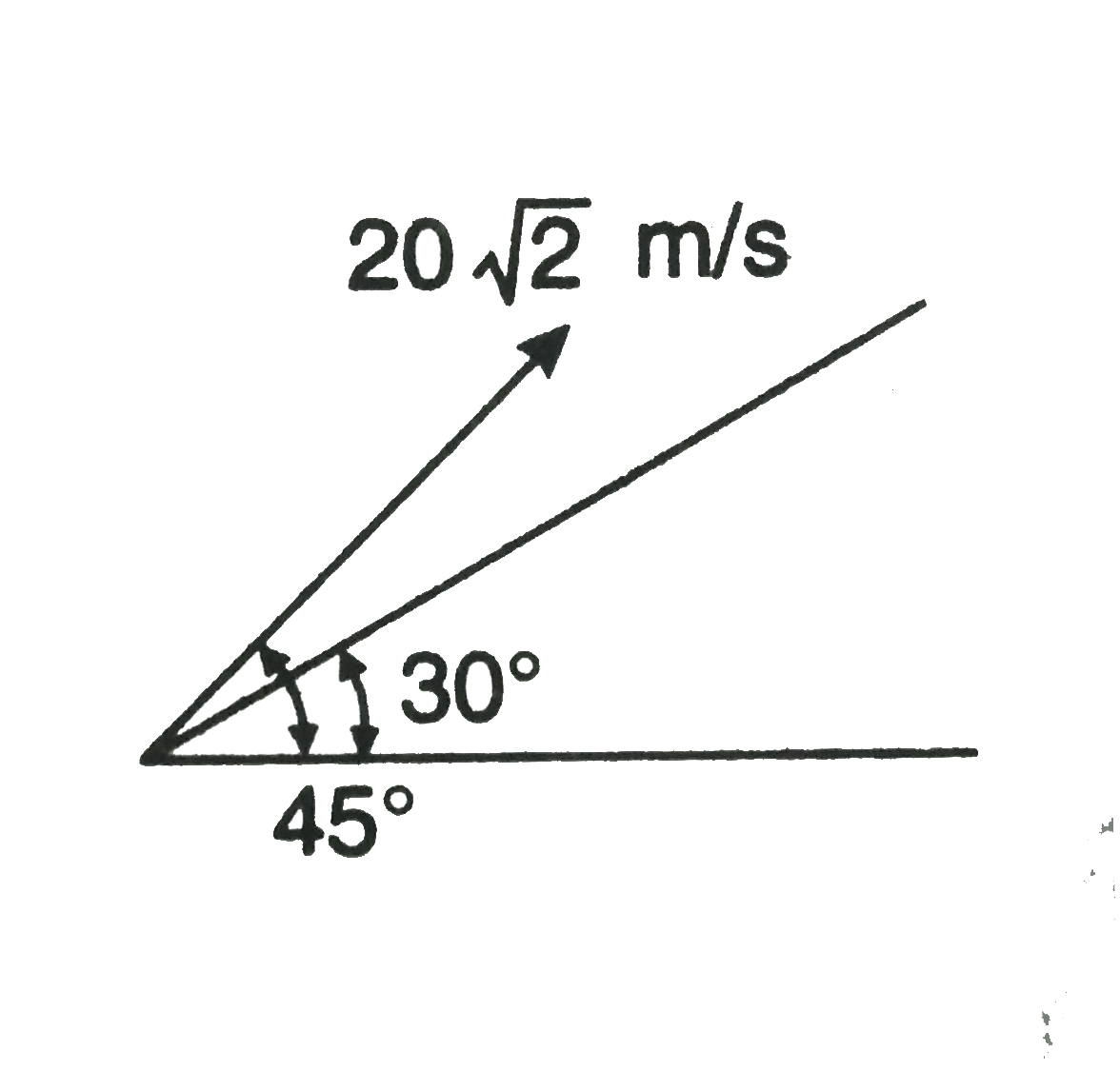
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
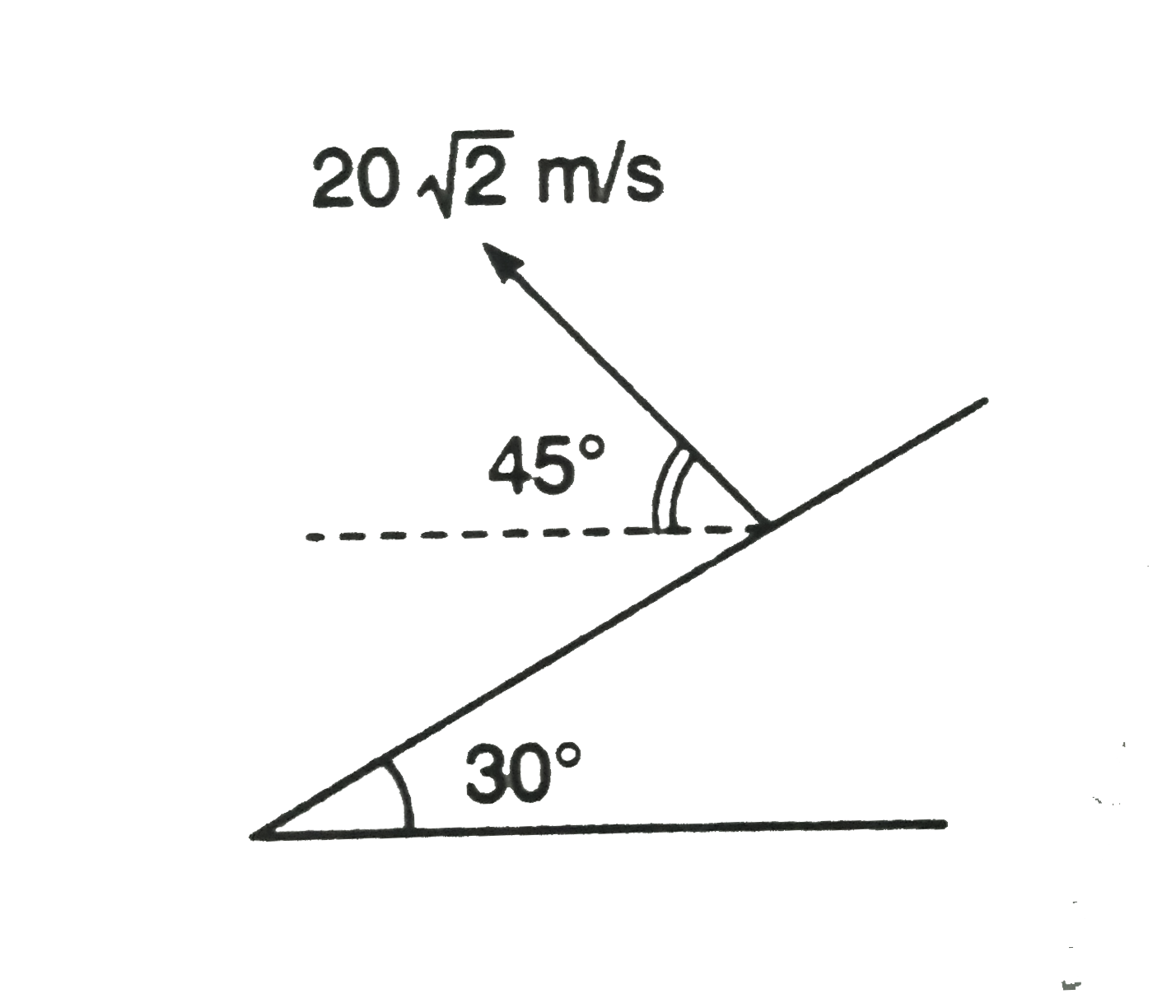
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.
View Solution


 .
.