A particle is projected from ground with velocity at from horizontal.
(a) Find the speed when velocity of the particle makes an angle of from horizontal.
(b) Find the time for the above situation.
(C ) Find the vertical height and horizontal distance of the particle from the starting point in the above position. Take .
The correct Answer is:A
Let's solve the problem step by step.
Given Data:
- Initial velocity, u=40m/s
- Angle of projection, θ=60∘
- Angle of interest, ϕ=37∘
- Acceleration due to gravity, g=10m/s2
Part (a): Find the speed when the velocity of the particle makes an angle of 37∘ from horizontal.
1. Calculate the horizontal and vertical components of the initial velocity:
- ux=ucosθ=40cos60∘=40×12=20m/s
- uy=usinθ=40sin60∘=40×√32=20√3m/s
2. At the point where the angle is 37∘:
- The horizontal component of the velocity remains constant:
Vx=ux=20m/s
3. Using the angle ϕ=37∘:
- The vertical component of the velocity at this point is:
Vy=Vsin(37∘)
- The speed V can be expressed as:
V=Vxcos(37∘)
- Since cos(37∘)≈0.8:
V=200.8=25m/s
Part (b): Find the time for the above situation.
1. Using the vertical motion equation:
Vy=uy−gt
- Substitute Vy=Vsin(37∘):
25sin(37∘)=20√3−10t
- Since sin(37∘)≈0.6:
25×0.6=20√3−10t
15=20√3−10t
- Rearranging gives:
10t=20√3−15
t=20√3−1510
- Calculate t:
t≈34.64−1510=1.964s
Part (c): Find the vertical height and horizontal distance of the particle from the starting point in the above position.
1. Vertical height h:
- Use the vertical motion equation:
h=uyt−12gt2
- Substitute uy=20√3 and t≈1.964:
h=20√3×1.964−12×10×(1.964)2
h≈34.64×1.964−5×3.866
h≈67.96−19.33≈48.63m
2. Horizontal distance x:
- Use the horizontal motion equation:
x=uxt
- Substitute ux=20:
x=20×1.964≈39.28m
Summary of Results:
- (a) Speed when the angle is 37∘: V≈25m/s
- (b) Time to reach that angle: t≈1.964s
- (c) Vertical height: h≈48.63m
- (c) Horizontal distance: x≈39.28m
- Initial velocity, u=40m/s
- Angle of projection, θ=60∘
- Angle of interest, ϕ=37∘
- Acceleration due to gravity, g=10m/s2
- ux=ucosθ=40cos60∘=40×12=20m/s
- uy=usinθ=40sin60∘=40×√32=20√3m/s
- The horizontal component of the velocity remains constant:
Vx=ux=20m/s
- The vertical component of the velocity at this point is:
Vy=Vsin(37∘)
- The speed V can be expressed as:
V=Vxcos(37∘)
- Since cos(37∘)≈0.8:
V=200.8=25m/s
Vy=uy−gt
- Substitute Vy=Vsin(37∘):
25sin(37∘)=20√3−10t
- Since sin(37∘)≈0.6:
25×0.6=20√3−10t
15=20√3−10t
- Rearranging gives:
10t=20√3−15
t=20√3−1510
- Calculate t:
t≈34.64−1510=1.964s
- Use the vertical motion equation:
h=uyt−12gt2
- Substitute uy=20√3 and t≈1.964:
h=20√3×1.964−12×10×(1.964)2
h≈34.64×1.964−5×3.866
h≈67.96−19.33≈48.63m
- Use the horizontal motion equation:
x=uxt
- Substitute ux=20:
x=20×1.964≈39.28m
- (a) Speed when the angle is 37∘: V≈25m/s
- (b) Time to reach that angle: t≈1.964s
- (c) Vertical height: h≈48.63m
- (c) Horizontal distance: x≈39.28m
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 2
1 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 3
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionA particle is projected from ground with velocity 40(√2)m/s at 45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
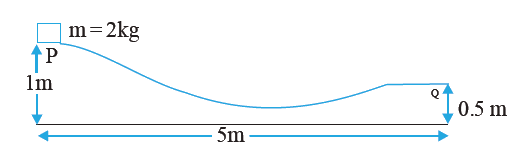
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View Solution
