A dielectric (k=3.2) is placed in a capacitor of distance 1m and area 2m2. The width of dielectric is 0.5m. If net capacitance is xε0
The correct Answer is:C, D
To solve the problem, we need to determine the net capacitance of a capacitor with a dielectric material inserted. Here are the steps to find the solution:
1. Identify the Parameters:
- Dielectric constant k=3.2
- Distance between plates D=1m
- Area of the plates A=2m2
- Width of the dielectric d=0.5m
2. Divide the Capacitor:
The capacitor can be thought of as two capacitors in series:
- Capacitor C1 (air gap): Distance = 0.5m
- Capacitor C2 (with dielectric): Distance = 0.5m
3. Calculate Capacitance of C1:
The formula for capacitance is given by:
C=Aϵ0kD
For C1 (with air, k=1):
C1=2ϵ0⋅10.5=4ϵ0
4. Calculate Capacitance of C2:
For C2 (with dielectric, k=3.2):
C2=2ϵ0⋅3.20.5=12.8ϵ0
5. Combine Capacitors in Series:
The total capacitance Cequiv for capacitors in series is given by:
1Cequiv=1C1+1C2
Substituting the values:
1Cequiv=14ϵ0+112.8ϵ0
6. Calculate the Right Side:
Finding a common denominator:
1Cequiv=3.2+112.8ϵ0=4.212.8ϵ0
7. Find Cequiv:
Inverting gives:
Cequiv=12.8ϵ04.2=3.05ϵ0
8. Determine Value of x:
Since we have Cequiv=xϵ0, we find:
x=3.05
Final Answer:
The value of x is approximately 3.05.
- Dielectric constant k=3.2
- Distance between plates D=1m
- Area of the plates A=2m2
- Width of the dielectric d=0.5m
The capacitor can be thought of as two capacitors in series:
- Capacitor C1 (air gap): Distance = 0.5m
- Capacitor C2 (with dielectric): Distance = 0.5m
The formula for capacitance is given by:
C=Aϵ0kD
For C1 (with air, k=1):
C1=2ϵ0⋅10.5=4ϵ0
For C2 (with dielectric, k=3.2):
C2=2ϵ0⋅3.20.5=12.8ϵ0
The total capacitance Cequiv for capacitors in series is given by:
1Cequiv=1C1+1C2
Substituting the values:
1Cequiv=14ϵ0+112.8ϵ0
Finding a common denominator:
1Cequiv=3.2+112.8ϵ0=4.212.8ϵ0
Inverting gives:
Cequiv=12.8ϵ04.2=3.05ϵ0
Since we have Cequiv=xϵ0, we find:
x=3.05
The value of x is approximately 3.05.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
In the figure a capacitor is filled with dielectrics K1,K2 and K3. The resultant capacitance is
View SolutionInside a parallel plate capacitor of width 'd' a di-electric plate with dielectric constant k & width 3d/4 is inserted the new capacitance is C'. Before insertion of dielectric the capacitance was C0. Find relation between C0&C'
View Solution
Knowledge Check
A capacitor consists of two parallel metal plates of area A separated by a distance d. A dielectric slab of area A, thickness b and dielectric constant k is placed inside the capacitor. If Ck is the capacitance of capacitor with dielectric, under what limits the values of k and b are to be restricted so thatCk=2C, where C is capacitance without dielectric?
Ak=4b2b−d & d3<b≤dBk=2b2b−d & d2<b≤dCk=2b2b−d & d2≤b≤2dDk=2b2b−d & d4≤b≤dA parallel plate capacitor with oil as a dielectric between the plates has a capacitance C. if the oil, with dielectric constannt (K=3), is removed, then the capacitance of the capacitor will be
A3CBC√3CC3D√3CA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.
 A(a) E1E2=1B(b) E1E2=1KC(c) Q1Q2=3KD(d) CC1=2+KK
A(a) E1E2=1B(b) E1E2=1KC(c) Q1Q2=3KD(d) CC1=2+KK
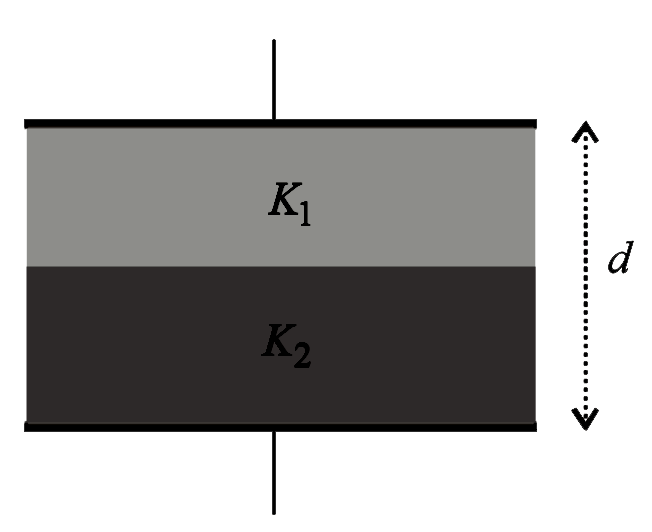
N dielectics are introduced in series in a capacitor of thickness D. Each dielectric have width d=D/N & dielectric constant of mth dielectric is given by Km=K(1+m/N). [Ngtgt103, Area of plates =A] . Net capacitance is given by Kε0AαDln2. find value of α
View SolutionA parallel plate capacitor having a separation between the plates d, plate area A and material with dielectric constant K has capacitance C0. Now one-third of the material is replaced by another material with dielectric constant 2K, so that effectively there are two capacitors one with area 1/3A, dielectric constant 2K and another with area 2/3A and dielectric constant K. If the capacitance of this new capacitor is C then CC0is
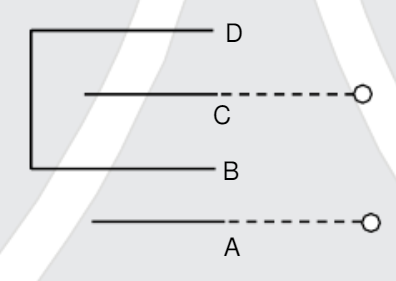
View SolutionFour parallel plates A,B,C,D each of length 2m, wdth 3/2m, are placed parallel to eachother at distance d. If B&D are now connected, the equivalent capacitance between A & C is xε0d Then value of x is
View SolutionA dielectric slab is introduced inside an uncharged capacitor of plate area A and plate separation L. The surface area of the slab is A and its thickness is slightly less than L. Let the surfaces of the slab that are facing the plates of the capacitor be called its two “faces”. The dielectric constant of the slab varies with distance x from one of its faces as: K=K0(1+XL), where K0 is a constant. After the insertion of the slab, the capacitance of the capacitor is n(K0ε0ALloge2). The value of n is _________.
View SolutionA capacitor of capacitance C=15pF is charged with voltage V=500V . The electric field inside the capacitor with dielectric is 106V/m and the area of the plate 10−4m2 , then the dielectric constant of the medium is : (.ε0=8.85×10−12 in S.I units) (A) 12.47 (B) 8.47 (C) 10.85 (D) 14.85
View Solution
