Consider the combination of 2 capacitors C1andC2 with C2>C1, when connected in parallel, the equivalent capacitance is 154 time the equivalent capacitance of the same connected in series. Calculate the ratio of capacitors,C2C1
1511
11180
2915
154
The correct Answer is:B
To solve the problem, we need to find the ratio of the two capacitors C2 and C1 given that when connected in parallel, the equivalent capacitance is 154 times the equivalent capacitance when connected in series.
Step 1: Write the equations for equivalent capacitance
1. Parallel Capacitance:
Cparallel=C1+C2
2. Series Capacitance:
Cseries=C1C2C1+C2
Step 2: Set up the relationship given in the problem
According to the problem, the equivalent capacitance in parallel is 154 times the equivalent capacitance in series:
C1+C2=154(C1C2C1+C2)
Step 3: Cross-multiply to eliminate the fraction
Multiply both sides by (C1+C2):
(C1+C2)2=154C1C2
Step 4: Expand and rearrange the equation
Expanding the left side:
C21+2C1C2+C22=154C1C2
Rearranging gives:
C21+2C1C2+C22−154C1C2=0
Step 5: Multiply through by 4 to eliminate the fraction
Multiplying everything by 4:
4C21+8C1C2+4C22−15C1C2=0
Step 6: Rearranging the equation
This simplifies to:
4C21+4C22−7C1C2=0
Step 7: Divide by C21
Let x=C2C1. Then C2=xC1:
4+4x2−7x=0
Step 8: Rearranging into standard quadratic form
This can be rearranged to:
4x2−7x+4=0
Step 9: Use the quadratic formula to find x
Using the quadratic formula x=−b±√b2−4ac2a:
x=7±√(−7)2−4⋅4⋅42⋅4
x=7±√49−648
x=7±√−158
Step 10: Analyze the discriminant
Since the discriminant is negative (−15), there are no real solutions for x. This means that under the given conditions, the ratio C2C1 does not exist.
Final Result
Thus, the ratio C2C1 cannot be determined under the given conditions.
---
Cparallel=C1+C2
Cseries=C1C2C1+C2
C1+C2=154(C1C2C1+C2)
(C1+C2)2=154C1C2
C21+2C1C2+C22=154C1C2
C21+2C1C2+C22−154C1C2=0
4C21+8C1C2+4C22−15C1C2=0
4C21+4C22−7C1C2=0
4+4x2−7x=0
4x2−7x+4=0
x=7±√(−7)2−4⋅4⋅42⋅4
x=7±√49−648
x=7±√−158
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS (SECTION-A)
Explore 20 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS SECTION B
Explore 30 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Knowledge Check
The effective capacitance of two capacitors of capacitances C1 and C2(C2>C1) connected in parallel is 256 times the effective capacitance when they are connected in series. The ratio C2C1 is
A32B43C53D256When a number of capacitor are connected in parallel between two points, the equivalent capacitance
AincreasesBdecreasesCremains the sameDnone of the aboveThe effective capacitance of two capacitors of capacitances C1 and C2(C2>C1) connected in parallel is 256 times the effective capacitance when they are connected in series. The ratio C2C1 is
A32B43C53D256
Find the equivalent capacitance between A and B. All the capacitors have capacitance C.

View SolutionTwo identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
View SolutionWhen two capacitors are connected in series, the equivalent capacitance is 1.2μF. When they are connected in parallel, the equivalent capacitance is 5μF. The capacitances of the capacitors are
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
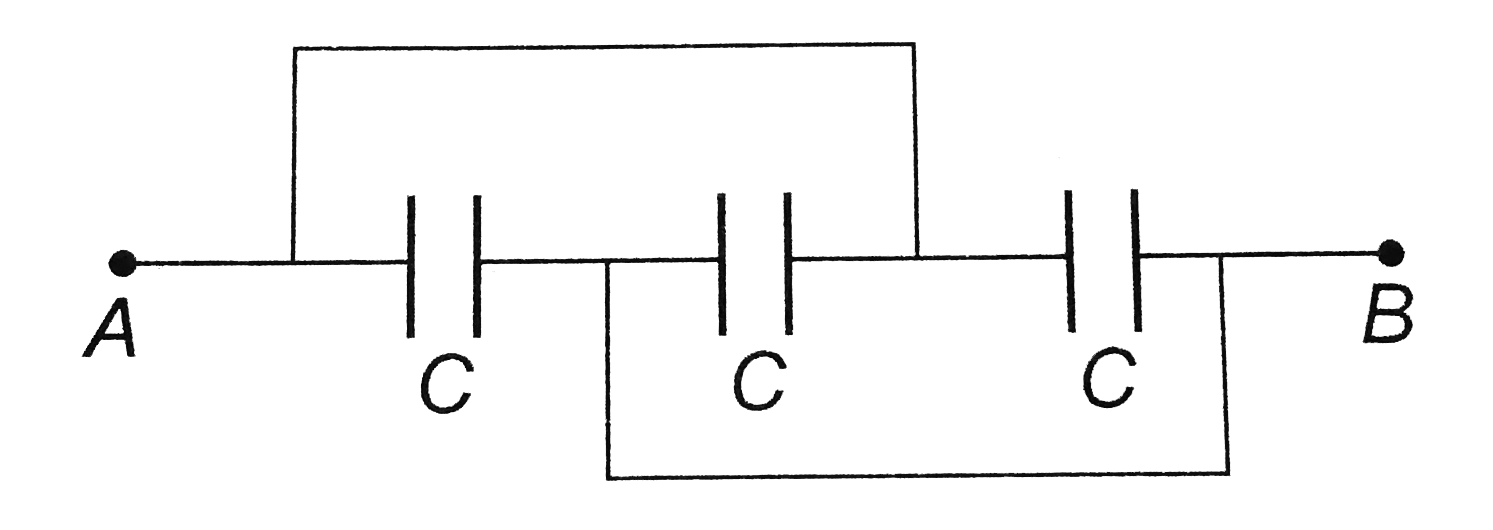
View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is

View Solution
