If two similar springs each of spring constant K1 are joined in series, the new spring constant and time period would be changed by a factor:
12,√2
14,√2
14,2√2
12,√2
The correct Answer is:A
To solve the problem of finding the new spring constant and time period when two similar springs, each with spring constant K1, are joined in series, we can follow these steps:
Step 1: Understanding Springs in Series
When two springs are connected in series, the total extension Xnet is the sum of the extensions of each spring. If X1 is the extension of the first spring and X2 is the extension of the second spring, then:
Xnet=X1+X2
Step 2: Relating Force and Extension
The force F applied to the system is the same for both springs. According to Hooke's Law, we have:
F=K1X1andF=K1X2
Thus, we can express the extensions as:
X1=FK1andX2=FK1
Step 3: Finding the Total Extension
Substituting the expressions for X1 and X2 into the equation for Xnet:
Xnet=FK1+FK1=2FK1
Step 4: Finding the Effective Spring Constant
The effective spring constant Knet for the series combination can be defined as:
Xnet=FKnet
Equating the two expressions for Xnet:
2FK1=FKnet
Cancelling F from both sides (assuming F≠0):
2K1=1Knet
Thus, we find:
Knet=K12
Step 5: Finding the Time Period
The time period T of a spring-mass system is given by:
T=2π√mK
For the initial spring constant K1:
T1=2π√mK1
For the new effective spring constant Knet=K12:
T2=2π√mKnet=2π√mK12=2π√2mK1=√2⋅T1
Step 6: Finding the Change Factor
The change factor for the spring constant is:
Factor for K=KnetK1=K12K1=12
The change factor for the time period is:
Factor for T=T2T1=√2
Final Answer
- The new spring constant changes by a factor of 12.
- The time period changes by a factor of √2.
When two springs are connected in series, the total extension Xnet is the sum of the extensions of each spring. If X1 is the extension of the first spring and X2 is the extension of the second spring, then:
Xnet=X1+X2
The force F applied to the system is the same for both springs. According to Hooke's Law, we have:
F=K1X1andF=K1X2
Thus, we can express the extensions as:
X1=FK1andX2=FK1
Substituting the expressions for X1 and X2 into the equation for Xnet:
Xnet=FK1+FK1=2FK1
The effective spring constant Knet for the series combination can be defined as:
Xnet=FKnet
Equating the two expressions for Xnet:
2FK1=FKnet
Cancelling F from both sides (assuming F≠0):
2K1=1Knet
Thus, we find:
Knet=K12
The time period T of a spring-mass system is given by:
T=2π√mK
For the initial spring constant K1:
T1=2π√mK1
For the new effective spring constant Knet=K12:
T2=2π√mKnet=2π√mK12=2π√2mK1=√2⋅T1
The change factor for the spring constant is:
Factor for K=KnetK1=K12K1=12
The change factor for the time period is:
Factor for T=T2T1=√2
- The new spring constant changes by a factor of 12.
- The time period changes by a factor of √2.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION B
30 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
A√k1k2B(k1+k2)2Ck1+k2Dk1k2(k1+k2)Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
A√k1k2B(k1+k2)/2Ck1+k2Dk1k2k1+k2A spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
Ak3B3kCkDk6
What will be the spring constant k of a. spring if length of the spring is made n times?
View SolutionA simple harmonic motion oscillator has two springs of spring constant k and other two of spring constant 2k, arranged as shown in the figure. Calculate the time period of oscillator.
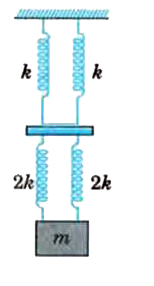
View SolutionA spring having a spring constant k is divded into three parts. Calculate the force constant for each part.
View SolutionA spring fo spring constant k is broken in the length ratio 1:3. The spring constant of larger part will be
View SolutionThe electrical analog of a spring constant k is
View Solution
