In ΔOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are Solution in Telugu
1:4,3:2
4:1,3:2
4:1,1:2
4:1,2:3
The correct Answer is:B
Step by step video, text & image solution for In DeltaOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - DOT PRODUCT OF TWO VECTORS
34 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - CROSS PRODUCT OF TWO VECTORS
17 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LINEAR EQUATIONS
13 Videos
- 3D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D-COORDINATE SYSTEMEXERCISE - PRACTICE EXERCISE
40 Videos
- CHANGE OF AXESBOOK - AAKASH SERIESCHAPTER - CHANGE OF AXESEXERCISE - Practice Exercise
29 Videos
Similar Questions
If AD, BE and CF are the medians of ΔABC, then the value of ¯¯¯¯¯¯BC.¯¯¯¯¯¯AD+¯¯¯¯¯¯CA.¯¯¯¯¯¯BE+¯¯¯¯¯¯AB.¯¯¯¯¯¯CF=
View SolutionLet ¯aand¯b be two non-collinear unit vectors. If ¯u=¯a−(¯a.¯b)¯band¯v=¯aׯb, then |¯v|=
View SolutionIf a+b+c≠0, the system of equations
(b+c)(y+z)−ax=b−c,
(c+a)(z+x)−by=c−a,
(a+b)(x+y)−cz=a−b has
View SolutionThe point (-1,4,-2) lie in the octant
View SolutionThe coordinates of the point (3,-5) in the new system when the origin is shifted to (-2,3) are
View SolutionIf D E and F be the mid ponts of the sides BC, CA and AB respectively of the △ABC and O be any point, then prove that −−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF
View SolutionE और F क्रमश: त्रिभुज ABC की बराबर भुजाओ AB और AC के मध्यें-बिंदु है दर्शाइए की BF=CE है
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the mid-points of opposite sides. If O be any point in the plane, then show that −−→OA+−−→OB+−−→OC+−−→OD=4−−→OE.
View SolutionIn ΔOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are
View SolutionIn a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?

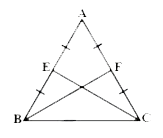
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
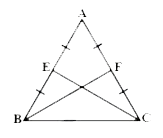
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
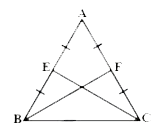
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
View Solution
