Assume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
The correct Answer is:B
To find the time period of a particle executing simple harmonic motion (SHM) in a tunnel dug along a chord of the Earth at a perpendicular distance R2 from the Earth's center, we can follow these steps:
Step 1: Understand the gravitational force inside the Earth
When a particle is inside a spherical shell of uniform density, the gravitational force acting on it is due only to the mass of the Earth that is at a radius smaller than the distance of the particle from the center.
Using the shell theorem, the gravitational force F acting on a particle of mass m at a distance r from the center of the Earth is given by:
F=−GM(r)r2m
where M(r) is the mass of the Earth enclosed within radius r.
Step 2: Calculate the mass M(r)
The mass M(r) of the Earth within radius r can be expressed as:
M(r)=ρ⋅43πr3
where ρ is the density of the Earth. The average density of the Earth can be calculated using:
ρ=M43πR3
where M is the total mass of the Earth and R is its radius.
Step 3: Substitute M(r) into the force equation
At a distance r=R2:
M(R2)=ρ⋅43π(R2)3=ρ⋅43π⋅R38=16M
Thus, the force acting on the particle at r=R2 becomes:
F=−G⋅16M(R2)2m=−G⋅16M⋅4R2m=−2GM3R2m
Step 4: Relate the force to SHM
The force can be expressed in terms of the displacement x from the equilibrium position:
F=−kx
where k is the spring constant. From the previous step, we have:
k=2GM3R2
Step 5: Find the time period of SHM
The time period T of SHM is given by:
T=2π√mk
Substituting for k:
T=2π√m2GM3R2=2π√3mR22GM
Step 6: Final expression for the time period
Thus, the final expression for the time period T is:
T=2π√3R22g
where g=GMR2 is the acceleration due to gravity at the surface of the Earth.
Conclusion
The time period of the particle executing SHM in the tunnel is:
T=2π√3R2g
When a particle is inside a spherical shell of uniform density, the gravitational force acting on it is due only to the mass of the Earth that is at a radius smaller than the distance of the particle from the center.
F=−GM(r)r2m
where M(r) is the mass of the Earth enclosed within radius r.
The mass M(r) of the Earth within radius r can be expressed as:
M(r)=ρ⋅43πr3
where ρ is the density of the Earth. The average density of the Earth can be calculated using:
ρ=M43πR3
where M is the total mass of the Earth and R is its radius.
At a distance r=R2:
M(R2)=ρ⋅43π(R2)3=ρ⋅43π⋅R38=16M
Thus, the force acting on the particle at r=R2 becomes:
F=−G⋅16M(R2)2m=−G⋅16M⋅4R2m=−2GM3R2m
The force can be expressed in terms of the displacement x from the equilibrium position:
F=−kx
where k is the spring constant. From the previous step, we have:
k=2GM3R2
The time period T of SHM is given by:
T=2π√mk
Substituting for k:
T=2π√m2GM3R2=2π√3mR22GM
Thus, the final expression for the time period T is:
T=2π√3R22g
where g=GMR2 is the acceleration due to gravity at the surface of the Earth.
The time period of the particle executing SHM in the tunnel is:
T=2π√3R2g
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Assume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View Solution
Knowledge Check
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√RgA tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
A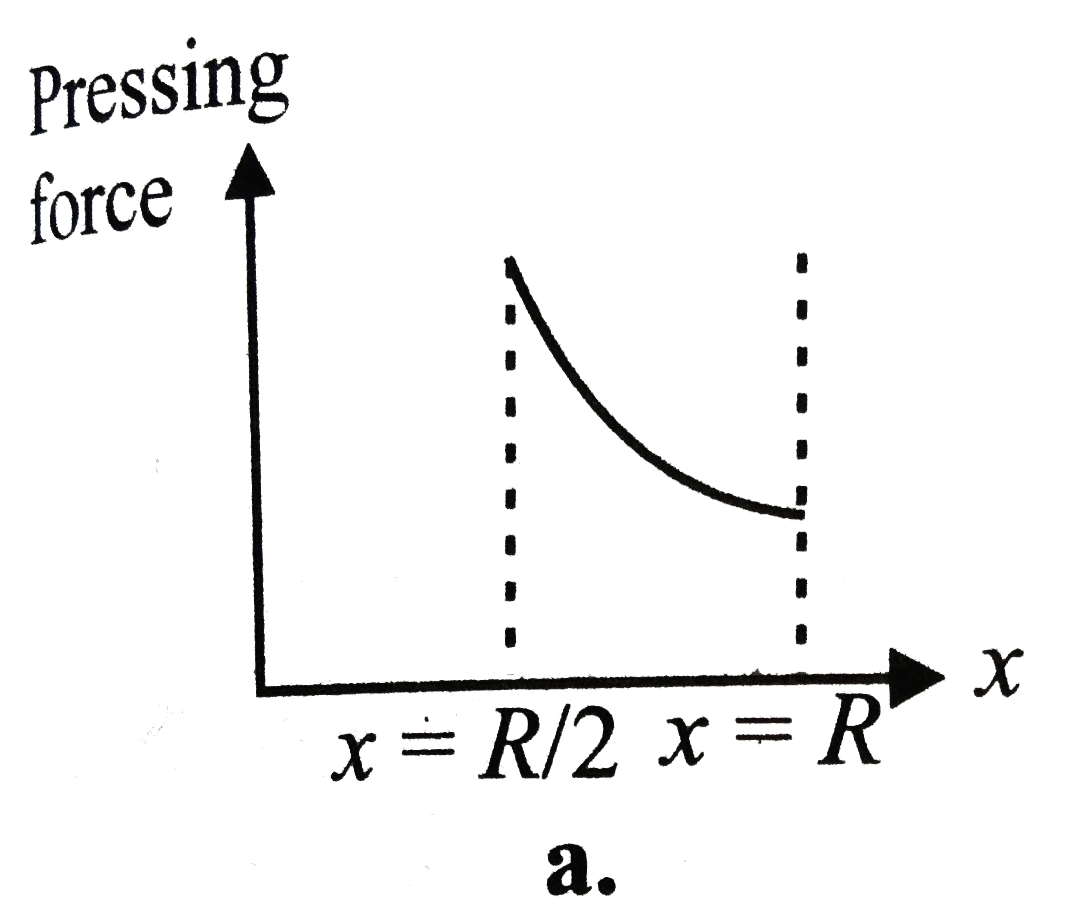 B
B C
C D
D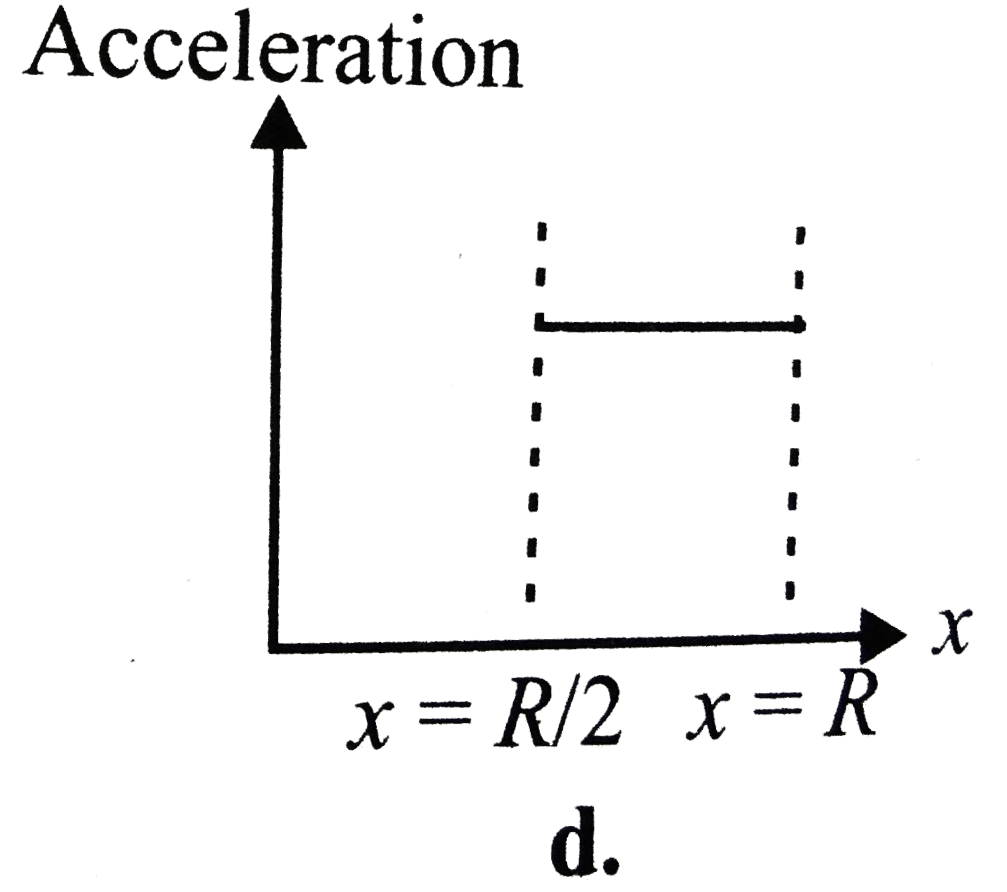
If a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toA2π√RgB2π√GMR3/2C84.6 minDNone of these
(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionA tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionImagine a smooth tunnel along a chord of nonrotating earth at a distance R2 from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V∘=√gR [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion.
View SolutionIf a tunnel is dug along the diameter of earth and a piece of stone is dropped into it, then the stone will
View SolutionIf a tunnel is dug along the diameter of the earth and a ball is dropped into the tunnel, it will have
View Solution

