Imagine a smooth tunnel along a chord of nonrotating earth at a distance R2 from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V∘=√gR [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion.
The correct Answer is:(a) NO
(b) rmax=(8+√5714)R
Step by step video, text & image solution for Imagine a smooth tunnel along a chord of nonrotating earth at a distance (R)/(2) from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V_(@)=sqrt(gR) [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Acceleration due to gravity at the centre of the earth is :-
AgBg2CzeroDinfiniteThe acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
A1/rB1/r2CrDr2Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
A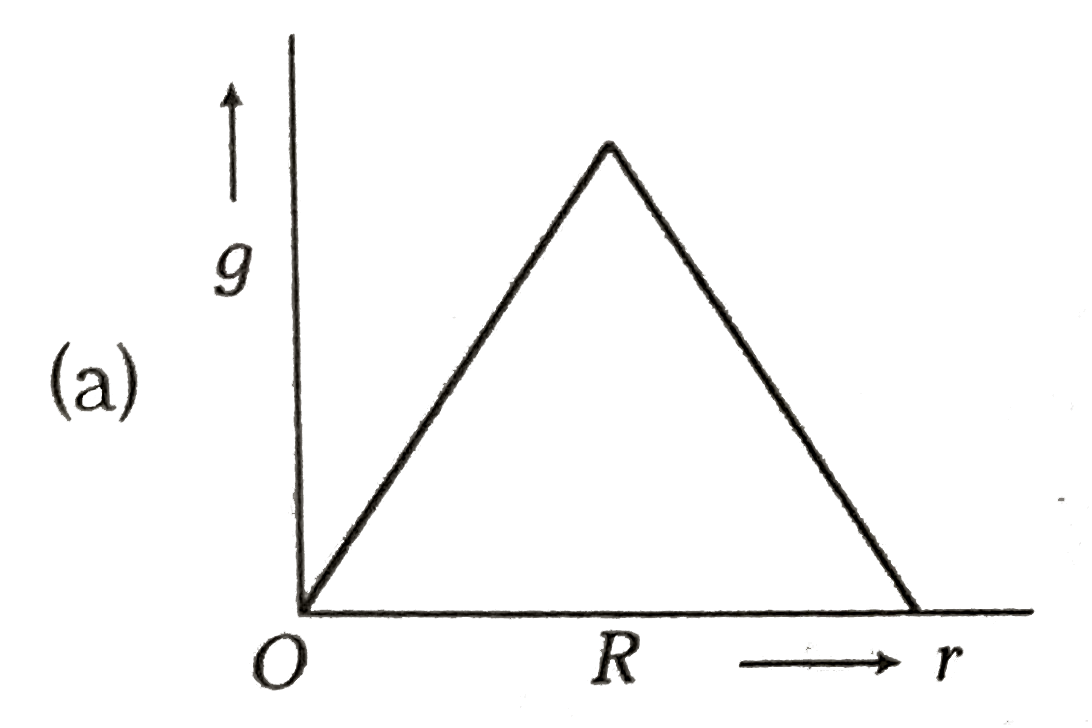 B
B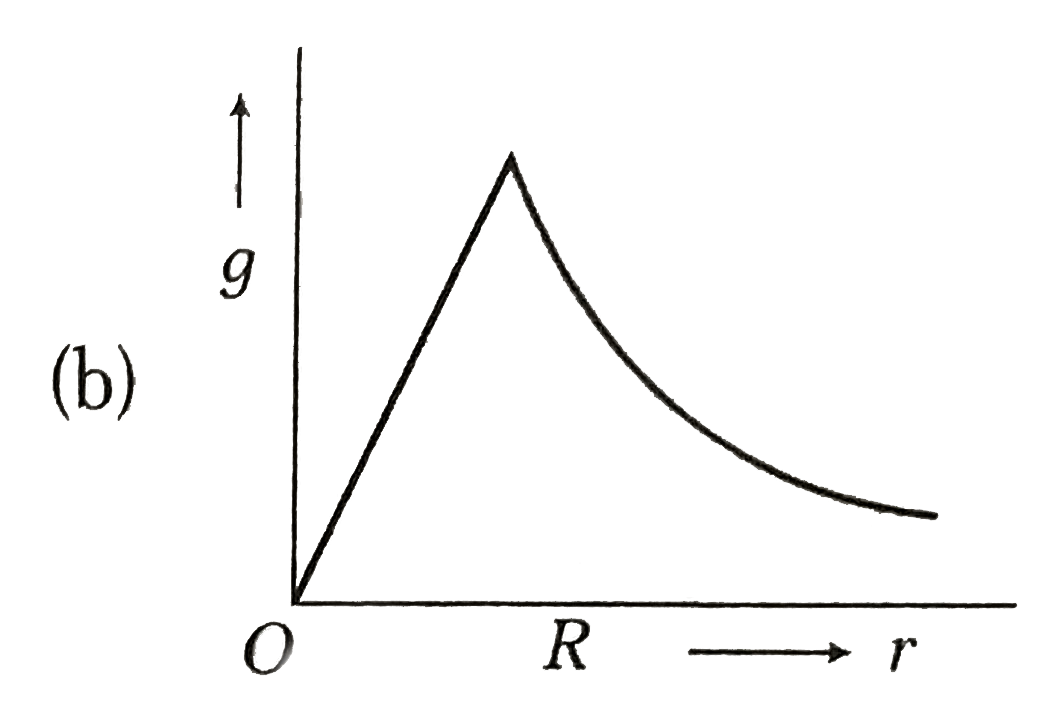 C
C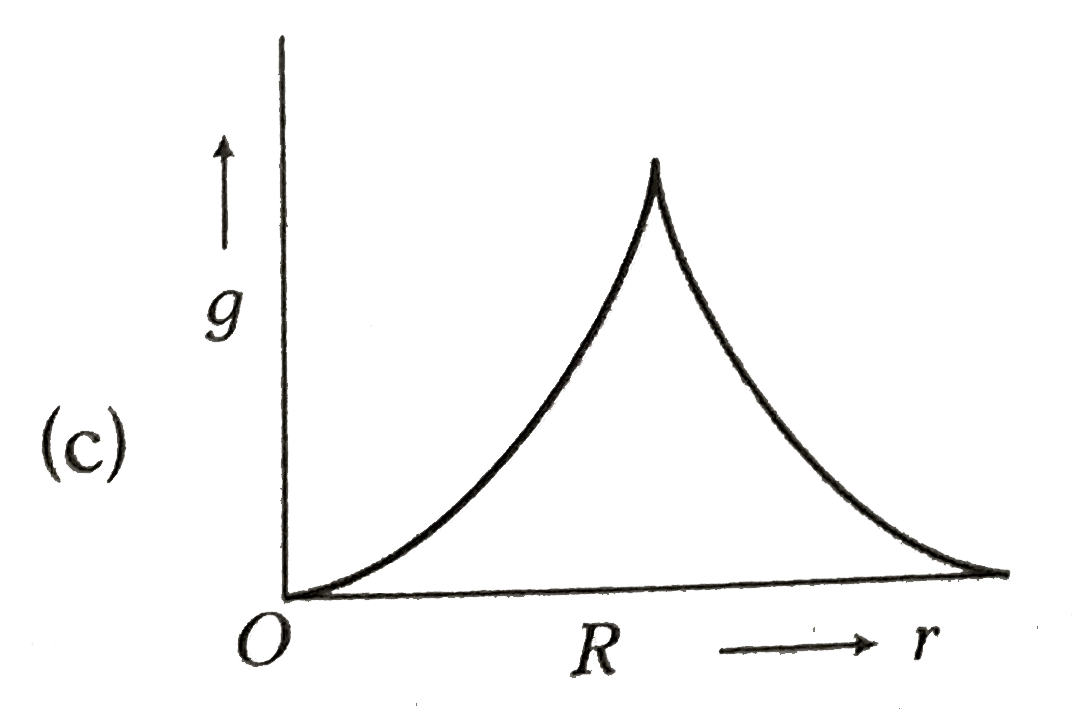 D
D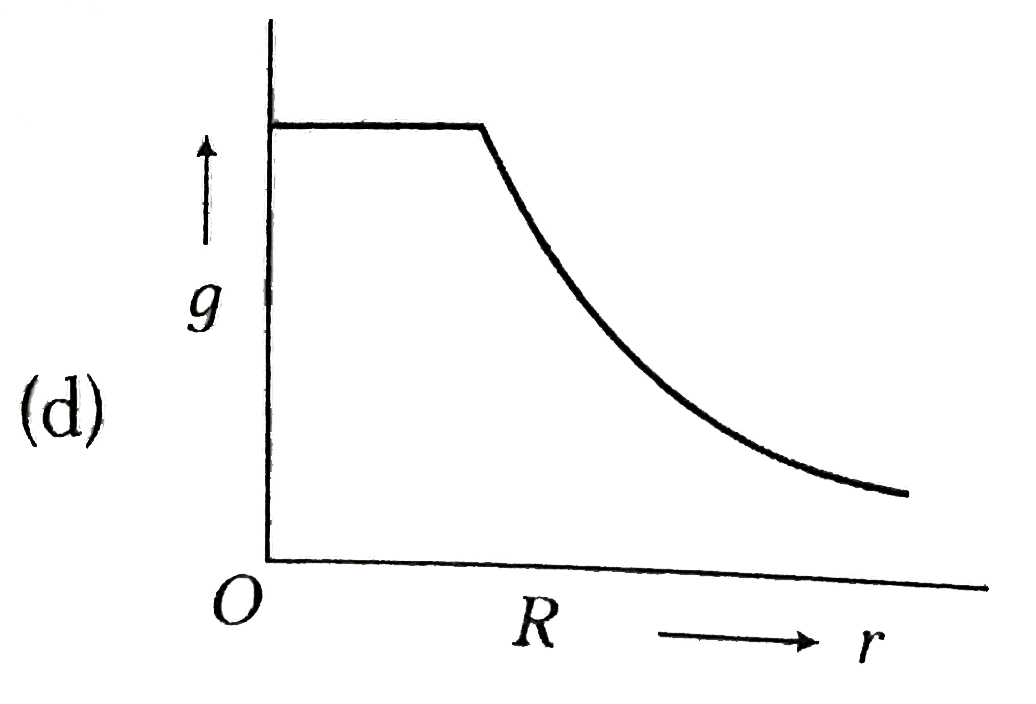
The earth has mass M and radius R .An object of mass m is dropped from a distance of 3R, from the centre of the earth.The object strikes the surface of the earth with a speed ,v=√kgR,where g is acceleration due to gravity or the surface of the earth.The value of k
View SolutionFind the acceleration due to gravity at a distance of 20000 kg from the centre of the earth.
View SolutionFind the acceleration due to gravity at a distance of 20000 km from the centre of the earth.
View SolutionStarting from the centre of the earth having radius R the variation of g (acceleration due to gravity) is shown by
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r>R) from the centre of the earth is proportional to
View Solution
