A bimetallic strip is formed out of two identical strips, one of copper and the other of brass. The coefficients of linear expansion of the two metals are αc and αB. On heating, the temperature of strip increases by ΔT and the strip bends to form an arc of radius R. Then R is proportional to Solution in Telugu
ΔT
1ΔT
√ΔT
1√ΔT
The correct Answer is:B
Step by step video, text & image solution for A bimetallic strip is formed out of two identical strips, one of copper and the other of brass. The coefficients of linear expansion of the two metals are alpha_(c) and alpha_(B). On heating, the temperature of strip increases by DeltaT and the strip bends to form an arc of radius R. Then R is proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-I (Straight Objective Type Questions) Mechanics & Elasticity application4videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Geometry Applications5videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (LECTURE SHEET) Integer Type Questions5videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
If a cylinder of diameter 1.0cm at 30°c is to be slide into a hole of diameter 0.9997 cm in a steel plate at the same temperature, then minimum required rise in the temperature of the plate is [coefficient of linear expansion of steel =12×10−6/∘C ]
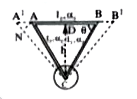
05:20View SolutionThe temperature compensated pendulum is designed to compensate for the change in length due to temperature rise. Figure shows one such pendulum. It consists of an isosceles triangular frame as shown in the figure. The pendulum is supported at mid-point of side AB, and it remains horizontal. Determine the ratio (l1/l2)2, so that the length of the pendulum remains same at all temperatures.
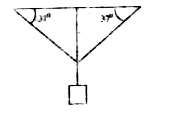
10:41View SolutionA block is hanged by means of two identical wires having cross-section area A (1mm2) as shown in the figure. If temperature is lowered by ΔT(10∘C), find the mass (in kg) to be added to hanging mass such that junction remains at its initial positions. Given that coefficient of linear expansion α=2×10−5I0C and Young's modulus Y=5×1011N/m2 for the wire.
05:04View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
04:32View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
02:02View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by ΔTand the strip bends to from an arc of radius of curvature R. Then R is.
04:26View SolutionTwo metal strips, each of length l and thickness d at temperature T0 are riveted together so that their ends coincide. One strip is made of metal A having a linear coefficient αB where αA>αB . When this bimetallic-strip is heated to a temperature (T0+ΔT) , one strip becomes longer than the other and the bimetallic strip bends into an arc of a circle. What is the radius of curvature R of the strip ?
04:43View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
08:11View SolutionTwo straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions are alpha_(1) "and" alpha_(2) . If they are heated through temperature DeltaT , the bimetallic strip will bend to form an arc of radius
View SolutionA bimetallic is made of two strips A and B having coefficients of linear expansion alpha_(4) and alpha_(B) . If alpha_(A) lt alpha_(B) , then on heating, the strip will
01:26View SolutionA bimetalic strip is made of two strips A and B, having co-efficeint of linear expansion as αA and αB. If αA>αB which of the following describes the behavior fo the metallic strip when heated?
View SolutionA bimetallic strip is formed out of two identical strips, one of copper and the other of brass. The coefficients of linear expansion of the two metals are αc and αB. On heating, the temperature of strip increases by ΔT and the strip bends to form an arc of radius R. Then R is proportional to
01:36View Solutionएक द्विघातु (Bimetallic strip) पट्टी दो समरूप पट्टियों से मिलकर बनी है, जिनमें से एक ताँबे की तथा दूसरी पीतल की है | दोनों धातुओं के रेखीय प्रसार गुणांक क्रमशः αC तथा αB है | गर्म करने पर , पट्टी का ताप ΔT बढ़ जाता है, तथा पट्टी R वक्रता त्रिज्या के चाप के आकार में मुड़ जाती है | R है
07:29View SolutionA bimetallic strip is formed out of identical strips one of copper and the other of brass. The coefficients of linear expansion of the two metals are alpha_(c) " and " alpha_(B). On heating the temperature of the strip goes up by DeltaT and the strip bends to form an arc of radius of curvature R. Then R is
02:07View SolutionTwo identical rectangular strips. One of copper and the other of steel, are riveted together to from a bimetallic strip. On heating. the strip will
(αcopper>αsteel)08:11View SolutionA bimetallic strip is formed out of two identical strips. One of copper and the other of brass. The coefficients of linear expansion of the two metals are αCandαB. On heating. the temperature of the strip goes up by ΔT and the strip bends to form a are of radius of curvature R. Then R is:
02:00View Solution