A thin brass sheet at and a thin stell sheet at have the same surface area. The common temperature at which both would have the same area is (coefficient of liner expansion for brass and steel are respectively and .Solution in Telugu
The correct Answer is:A
Step by step video, text & image solution for A thin brass sheet at 10^(@)C and a thin stell sheet at 20^(@)C have the same surface area. The common temperature at which both would have the same area is (coefficient of liner expansion for brass and steel are respectively 19xx10^(-6//@)C and 11xx10^(-6//@)C). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-I (Straight Objective Type Questions) Mechanics & Elasticity application
Explore 4 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Geometry Applications
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Integer Type Questions
Explore 5 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH SERIESChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE EXERCISE
Explore 99 Videos
- THERMODYNAMICSBook:AAKASH SERIESChapter:THERMODYNAMICSExercise:EXERCISE - 3
Explore 33 Videos
Similar Questions
If a cylinder of diameter 1.0cm at 30°c is to be slide into a hole of diameter 0.9997 cm in a steel plate at the same temperature, then minimum required rise in the temperature of the plate is [coefficient of linear expansion of steel =12×10−6/∘C ]
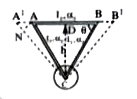
View SolutionThe temperature compensated pendulum is designed to compensate for the change in length due to temperature rise. Figure shows one such pendulum. It consists of an isosceles triangular frame as shown in the figure. The pendulum is supported at mid-point of side AB, and it remains horizontal. Determine the ratio (l1/l2)2, so that the length of the pendulum remains same at all temperatures.
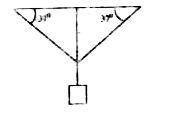
View SolutionA block is hanged by means of two identical wires having cross-section area A (1mm2) as shown in the figure. If temperature is lowered by ΔT(10∘C), find the mass (in kg) to be added to hanging mass such that junction remains at its initial positions. Given that coefficient of linear expansion α=2×10−5I0C and Young's modulus Y=5×1011N/m2 for the wire.
View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
View SolutionThe length of s steel rod exceeds that of a brass rod by 5 cm. If the difference in their lengths remains same at all temperature, then the length of brass rod will be: (α for iron and brass are 12×10−6/∘C and 18×10−6/∘C, respectively)
View SolutionA steel sheet at 20∘C has the same surface area as a brass sheet at 10∘C . If the coefficient of linear expansion of steel is 11×10−6/K and that of bross is 19×10−6/K , the common temperature at which both the sheets would have the same surface area is
View SolutionA thin brass sheet at 10∘C and a thin steel sheet at 20∘C have the same surface area. The common temperature at which both would have the same area is (Coefficient of linear expansion for brass and steel are respectively, 19×10−6/∘C are 11×10−6/∘C)
View SolutionA brass sheet is 25cm long and 8cm breath at 0∘C. Its area at 100∘C is (α=18×10−6/∘C)
View SolutionA thin brass sheet at 20^(@)C and a thin steel sheet at 30^(@)C have the same surface area. The common tempreture at which both would have the same area is (Coefficient of linear expansion for brass and steel are respectively, 19xx10^(-6)//^(@)C are 11xx10^(-6)//^(@)C )
View SolutionA steel rod is 4000cm in diameter at 30^(@)C A brass ring has an interior diameter of 3.992cm at 30^(@) in order that the ring just slides onto the steel rod the common temperature of the two should be nearly (alpha_(steel)=11xx10^(-6)/(^(@)C) and alpha_(brass)=19xx10^(-6)/(^(@)C)
View SolutionA sheet of brass is 40 cm long and 8 cm broad at 0^(@)C . If the area at 100^(@)C is 320.1m^(2) , calculate the coefficient of linear expansion of brass.
View SolutionA thin brass sheet at 10∘C and a thin stell sheet at 20∘C have the same surface area. The common temperature at which both would have the same area is (coefficient of liner expansion for brass and steel are respectively 19×10−6/∘C and 11×10−6/∘C).
View SolutionA barometer having a brass scale reads 77.24 cm at a temperature of 20^(@)C . The scale is graduated to be accurate at 0^(@)C . What would be the readint at 0^(@)C ? Coefficient of cubical expansion of mercury =18xx10^(-5).^(@)C^(-1) and linear expansion of brass -19xx10^(-6).^(@)C^(-1)
View SolutionConsider a brass rod and a steel rod (80 cm longer than brass rod) at 0^(@)C . It is observed that on increasing temperatures of the two rods by same amount difference in lengths of the two rods does not change. Given that the thermal coefficient of linear expansion for steel and brass are 11xx10^(-6).^(@)C^(-1) and 19xx10^(-6).^(@)C^(-1) respectively. The sum of lengths of the two rods at 0^(@)C is
View SolutionCoefficient of linear expansion of brass is 19×10−6∘C−1. If the area of a circular brass disc at 0∘C is 25 cm2, then at 80∘C its area will be
View Solution

