A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
proportional to ΔT
inversely proportional to ΔT
proportional to |αB−αC|
Inversely proportional to |αB−αC|
The correct Answer is:D
Co-efficient of linear expansion of brass is greater than that of copper i.e. αB>αC
∴LB=L0(1+αBΔT)
or (R+d)θ=L0(1+αBΔT)
Again, LC=L0(1++αCΔT)
or Rθ=L0(1+αCΔT)
∴(R+d)θRθ=1+αBΔT1+αCΔT
_E01_079_S01.png)
or R+dR=(1+αBΔT)(1−αCΔT), by binomial approximation
or 1+dR=1+(αB−αC)ΔT - Smaller terms
or dR=(αB−αC)De<T or R=d(αB−αCΔT)
∴R∝1ΔT Option (b) is correct. and
R∝1|αB−αC|. Option (d) is correct
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - VI
4 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - I (H.W.)
22 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-II (C.W.)
27 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
Similar Questions
A bimetallic strip is made up of two metals with different α
View SolutionTwo straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View Solution
Knowledge Check
A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by ΔTand the strip bends to from an arc of radius of curvature R. Then R is.
Aproportional to ΔTBinversely proportional to ΔTCproportional to |αB−αC|Dinversely proportional to |αB−αC|A bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
ABend with A on outer sideBBend with B on outer sideCNot bend at allDNone of the aboveA bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
ABend with A on outer sideBBend with B on outer sideCNot bend at allDNone of the above
Two indentical recrangular strips. One of copper and the other of steel, are rivetted together to from o bimetallic strip (αcopper>αsteel). On hearing. This strip will
View SolutionA bimetalic strip is made of two strips A and B, having co-efficeint of linear expansion as αA and αB. If αA>αB which of the following describes the behavior fo the metallic strip when heated?
View SolutionTwo mettalic strips each of length l0 and thickness d, temperature T0 are riveted together so that their ends coincide. One strip is maxe of a metal of coeficient of expansioin α1 and the other of a metal with a coefficient α2, where α2>α1. When this bimetallic strip is heated to a temperature T0+ΔT, find the radius of curvature R of the strip.
View SolutionA bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion α1 and α2 each of small thickness d and length L0 at T0. They are bonded together and, with a change in temperature De<AT, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be
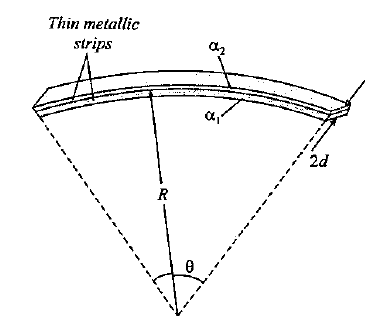
R=d(α2−α1)ΔT
View SolutionA bimetallic strip is composed of two identical strips, one of steel and other of brass. When the temperature of the strip is raised by ΔT , it bends to form arc of curvature R. If the coefficients of linear expansion of steel and brass are α1 and α2 , respectively, then R is
View Solution
