A bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion α1 and α2 each of small thickness d and length L0 at T0. They are bonded together and, with a change in temperature De<AT, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be
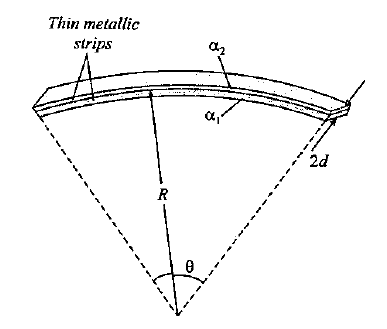
R=d(α2−α1)ΔT
Step by step video & image solution for A bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion alpha_(1) and alpha_(2) each of small thickness d and length L_(0) at T_(0). They are bonded together and, with a change in temperature DeltAT, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be R=d/((alpha_(2)-alpha_(1))DeltaT) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT
Explore 24 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
Similar Questions
The coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
View SolutionTwo rods of different metals of coefficient of linear expansion α1 and α2 and initial length l1 and l2 respectively are heated to the same temperature. Find relation in α1,α2,l1 and l2such that difference between their lengths remain constant.
View Solution
Knowledge Check
If L1 and L2 are the lengths of two rods of coefficients of linear expansion α1 and α2 respectively the condition for the difference in lengths to be constant at all temperatures is
AL1α1=L2α2BL1α2=L2α1CL1α1=L2α2DL1α2=L2α1The coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
A(α1+α22)lΔTB(α1+α2)lΔTC(α1+α22)lΔTD(α12+α2)lΔTA solid rectangular sheet has two different coefficients of linear expansion α1and α2 along its length and breadth respectively. The coefficient of surface expansion is (for α1t<<1,α2<<1)
Aα1+α22B2(α1+α2)C4α1α2α1+α2Dα1+α2
Two straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View SolutionTwo different wirese having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coeficient of linear expansion is :
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View Solution

