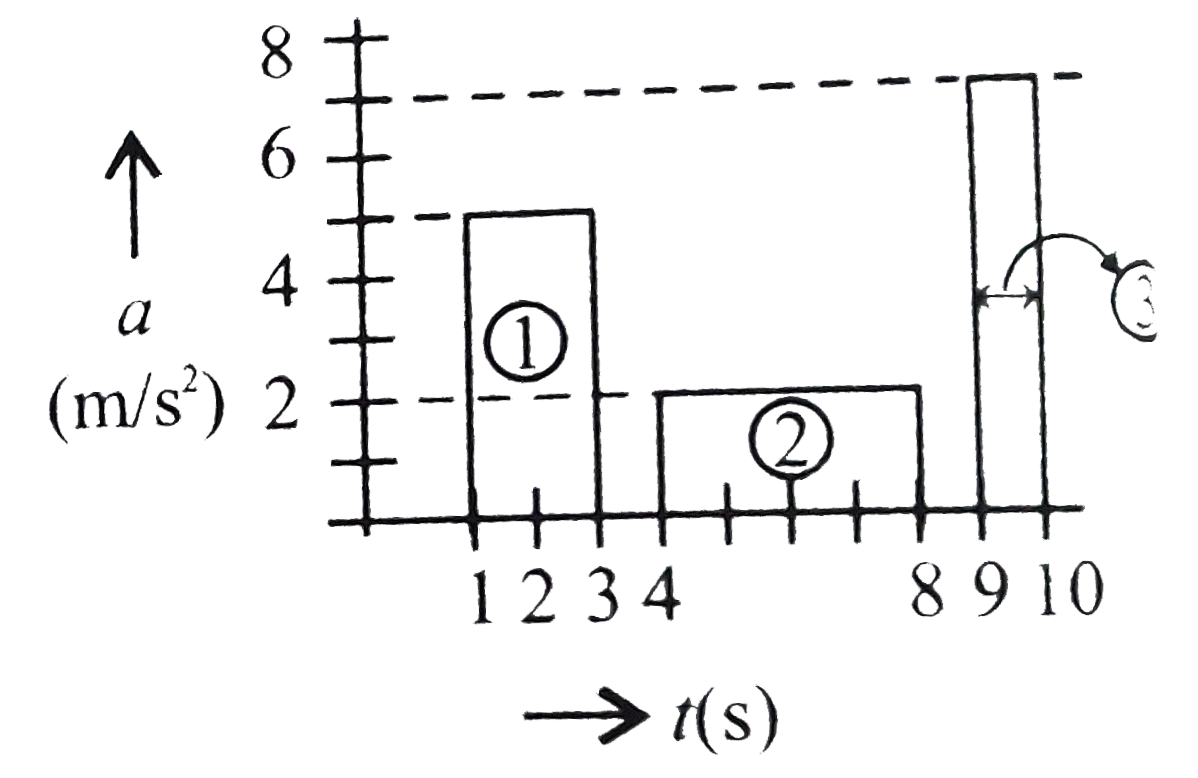
The figure shows a particle moving along x - axis subjected to three particles of acceleration (a). Rank the periods according to the increase they produce in the particle velocity, greatest first.
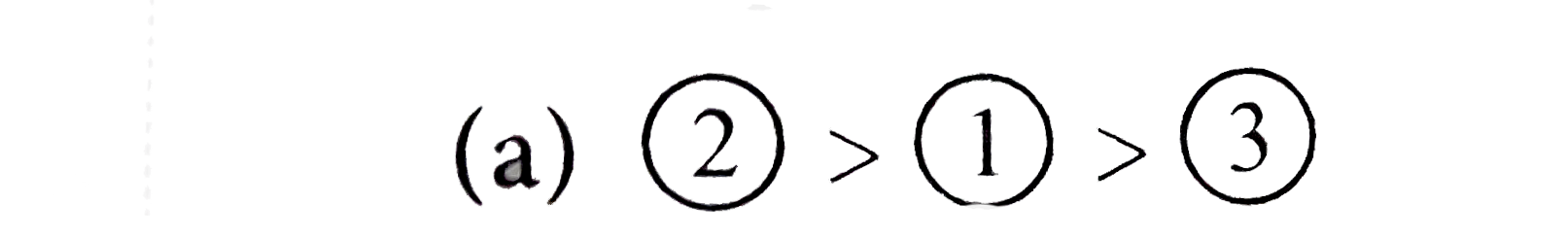

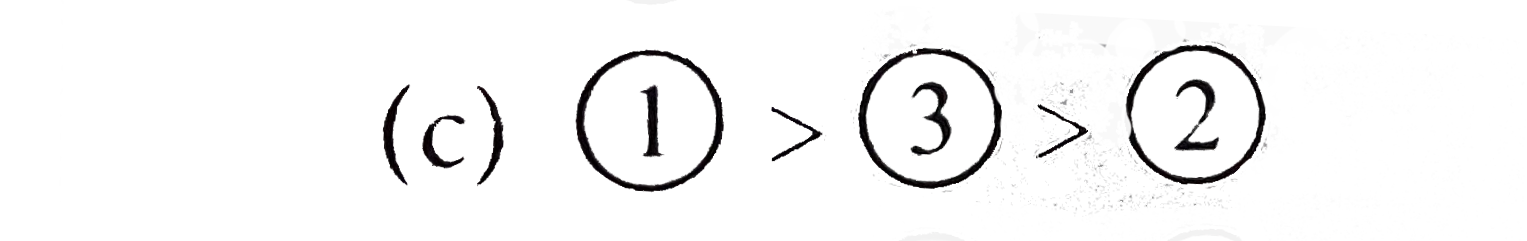
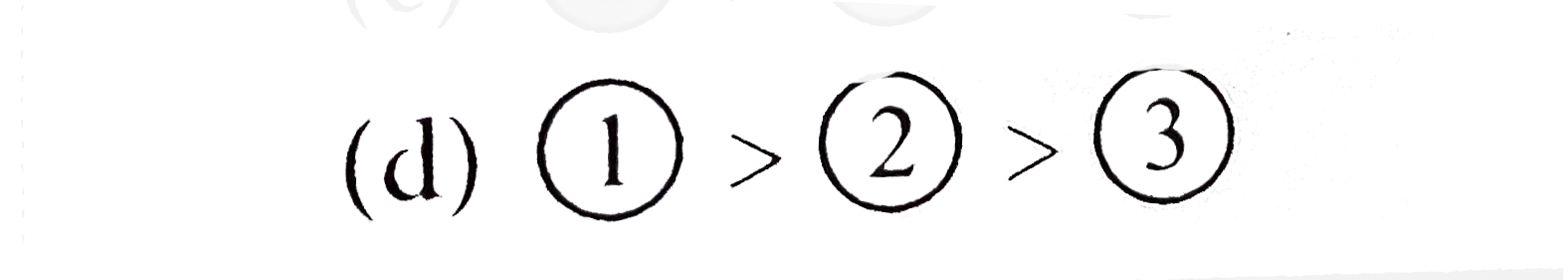
The correct Answer is:D
Area of acceleration-time graph gives velocity. Area of region gives velocity of particles ms−1
v1=2s×5ms2=10ms−1
Similarly, v2=4s×(2)m/s2=8m/s
and v3=1s×7m/s2 = 7m/s
∴v1>v2>v3
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - INSTANTANEOUS VELOCITY AND SPEED
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
For a particle moving along x−axis, speed must be increasing for the following graph :
View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
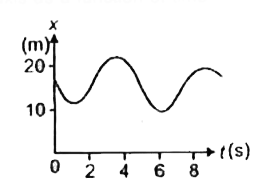
View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.

View SolutionThe speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionFor a particle moving along x-axis, a scaled x-6 graph is shown in figure. Mark the correct statement (s).
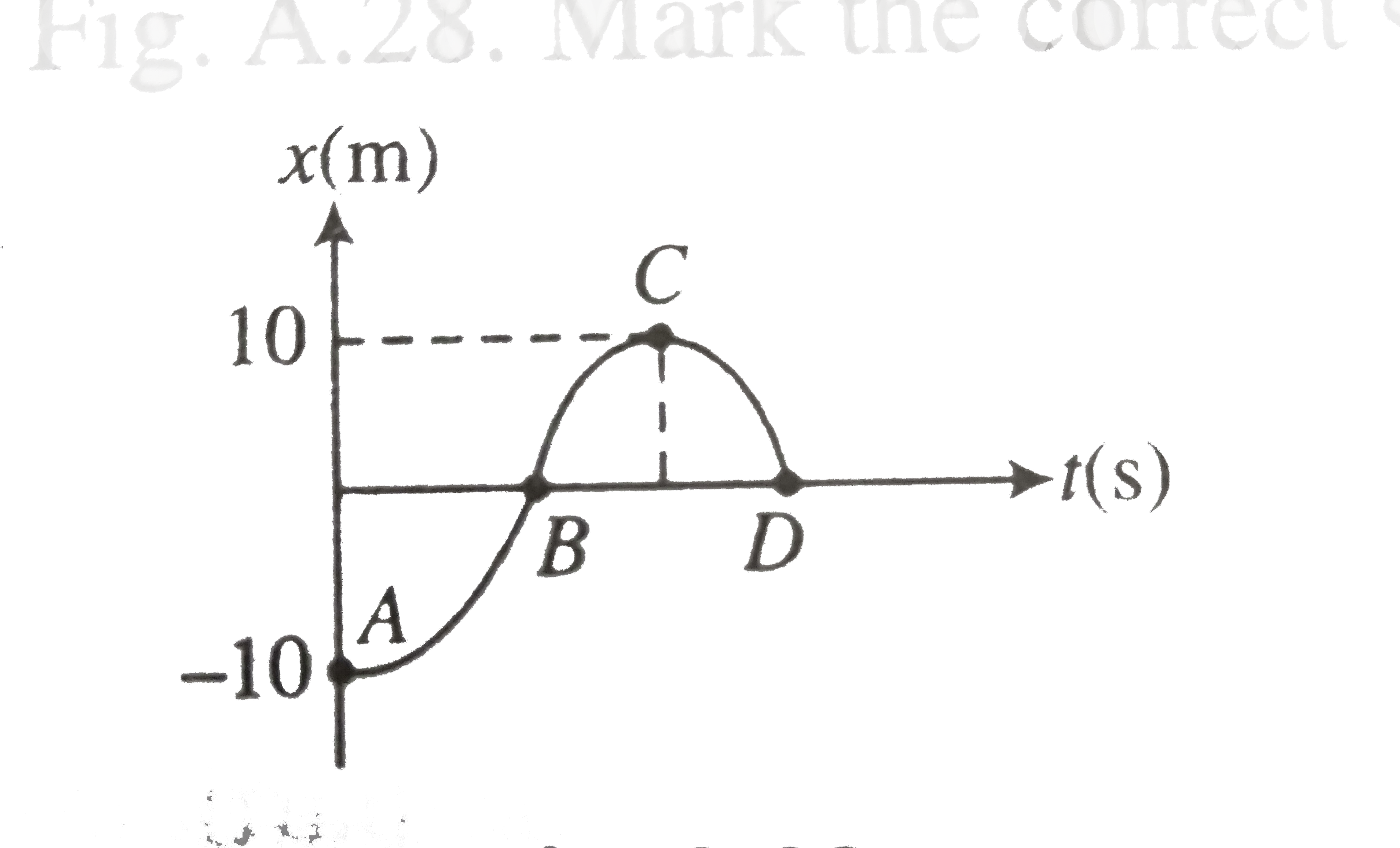
View SolutionA particle moved along the X−axis according to the graph shown in Figure. Choose the incorrct options.

View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
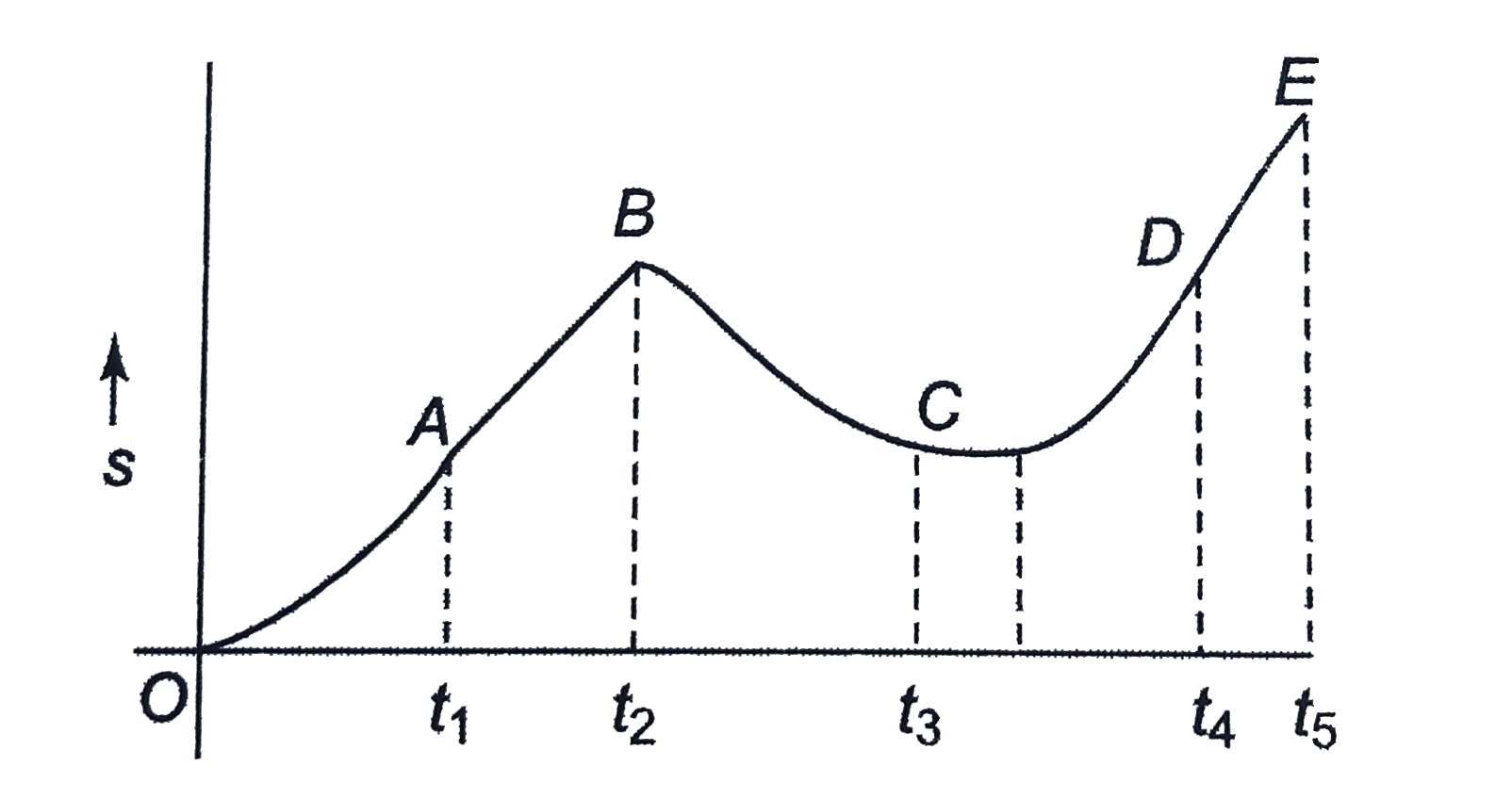
View Solution
