A particle moving along a straight line has a velocity v ms−1, when it cleared a distance of x m. These two are connected by the relation v = √49+x. When its velocity is 1ms−1, its acceleration is
2ms−2
7ms−2
1ms−2
0.5ms−2
The correct Answer is:D
To solve the problem step by step, we start with the given relationship between velocity v and displacement x:
Step 1: Understand the relationship
The relationship given is:
v=√49+x
Step 2: Differentiate the velocity with respect to displacement
To find the acceleration, we will use the formula:
a=vdvdx
First, we need to differentiate v with respect to x. We can rewrite v as:
v=(49+x)1/2
Now, we differentiate using the chain rule:
dvdx=12(49+x)−1/2⋅d(49+x)dx
Since the derivative of 49+x with respect to x is 1, we have:
dvdx=12√49+x
Step 3: Substitute back into the acceleration formula
Now we substitute dvdx back into the acceleration formula:
a=v⋅dvdx=v⋅12√49+x
Step 4: Substitute v in the acceleration equation
From the relationship v=√49+x, we can substitute v into the acceleration formula:
a=√49+x⋅12√49+x=12
Step 5: Conclusion
Thus, the acceleration a when the velocity v=1m/s is:
a=0.5m/s2
The relationship given is:
v=√49+x
To find the acceleration, we will use the formula:
a=vdvdx
First, we need to differentiate v with respect to x. We can rewrite v as:
v=(49+x)1/2
Now, we differentiate using the chain rule:
dvdx=12(49+x)−1/2⋅d(49+x)dx
Since the derivative of 49+x with respect to x is 1, we have:
dvdx=12√49+x
Now we substitute dvdx back into the acceleration formula:
a=v⋅dvdx=v⋅12√49+x
From the relationship v=√49+x, we can substitute v into the acceleration formula:
a=√49+x⋅12√49+x=12
Thus, the acceleration a when the velocity v=1m/s is:
a=0.5m/s2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - INSTANTANEOUS VELOCITY AND SPEED
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
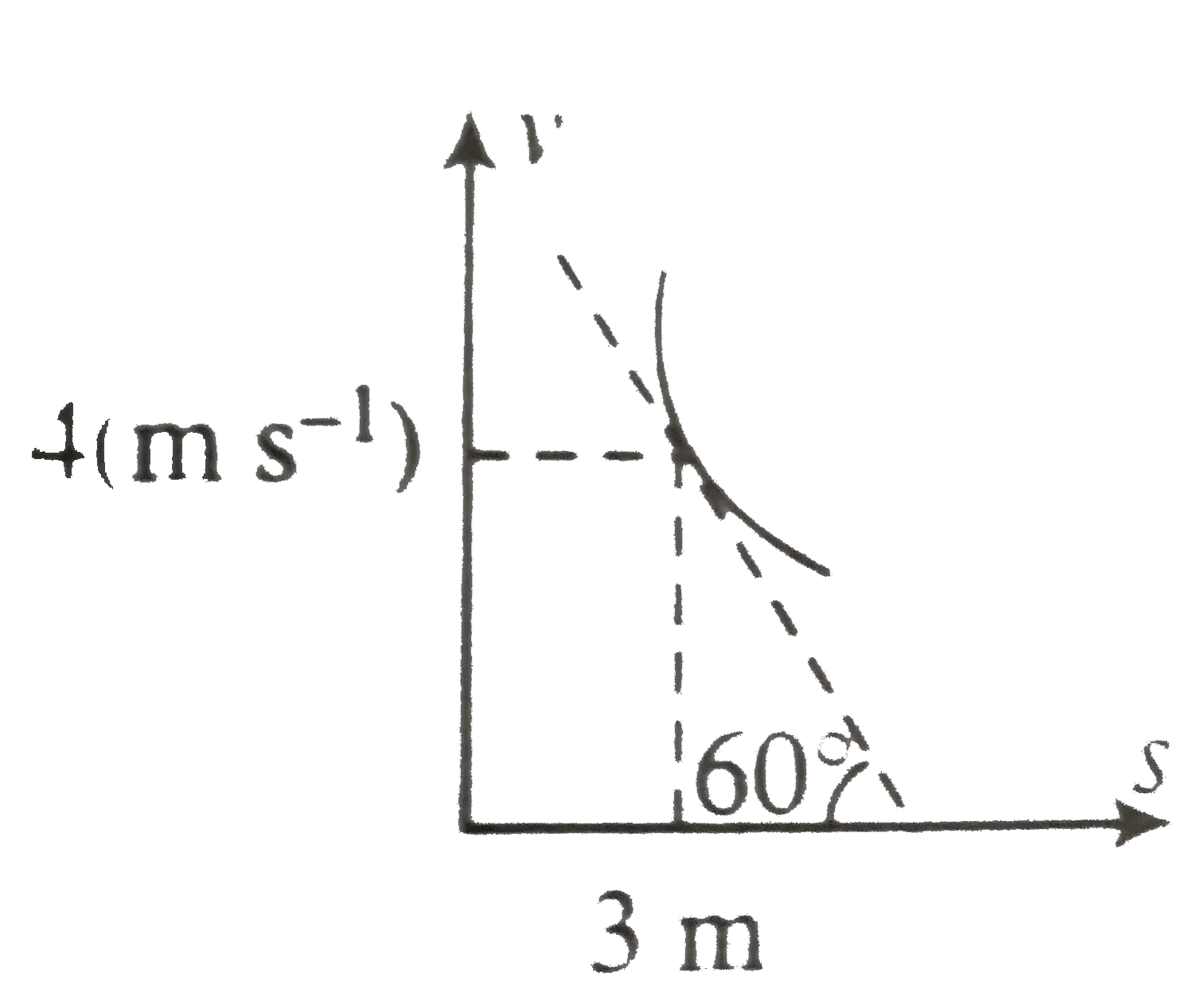
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionA particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Velocity of particle when acceleration is zero is :
View SolutionA particle moving in a straight line has velocity-displacement equation as v=5√1+s. Here v is in ms−1 and s in metres. Select the correct alternative.
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA body executing S.H.M.along a straight line has a velocity of 3ms−1 when it is at a distance of 4m from its mean position and4ms−1 when it is at a distance of 3m from its mean position.Its angular frequency and amplitude are
View SolutionA particle moving with uniform acceleration has its final velocity (v=√150+8x) m/s where x is the distance travelled by the body. Then the acceleration is
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA particle moves along a straight line with a variable acceleration given in the acceleration - displacement (a−S) curve as shown in the figure. Determine the velocity (in ms−1) of the particle after it has travelled a distance of 30 m. The initial velocity is 10 ms−1.
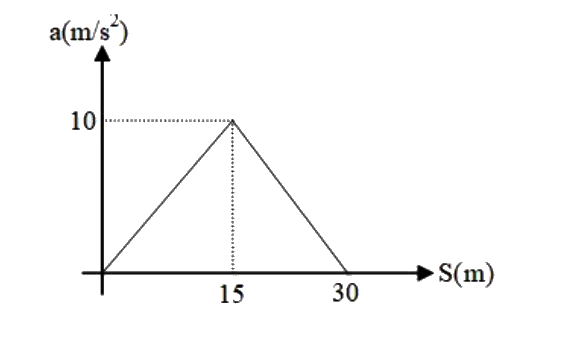
View Solution
