A convex refracting surface of radius of curvature separates two media of refractive indices . An object is placed in the first medium at a distance of from the refracting surface. Calculate the position of image formed.
The correct Answer is:B
To solve the problem of finding the position of the image formed by a convex refracting surface, we can follow these steps:
Step 1: Identify the Given Values
- Refractive index of the first medium (n1) = 4/3
- Refractive index of the second medium (n2) = 1.60
- Radius of curvature (R) = 20 cm (for a convex surface, R is positive)
- Object distance (u) = -200 cm (the object distance is negative as per the sign convention)
Step 2: Use the Refraction Formula
For a spherical refracting surface, the formula is given by:
−n1u+n2v=n2−n1R
Step 3: Substitute the Known Values into the Formula
Substituting the values we have:
−4/3−200+1.6v=1.6−4/320
Step 4: Simplify the Left Side
Calculating the left side:
4/3200=4600=1150
So, we have:
1150+1.6v=1.6−1.333320
Calculating 1.6−1.3333:
1.6−1.3333=0.2667
Now substituting this into the equation:
1150+1.6v=0.266720
Step 5: Calculate the Right Side
Calculating the right side:
0.266720=0.013335
Step 6: Rearranging the Equation
Now we have:
1.6v=0.013335−1150
Calculating 1150:
1150=0.0066667
So, substituting this value:
1.6v=0.013335−0.0066667=0.0066683
Step 7: Solve for v
Now, rearranging gives:
v=1.60.0066683≈240.00 cm
Conclusion
The position of the image formed is approximately 240 cm from the refracting surface.
---
- Refractive index of the first medium (n1) = 4/3
- Refractive index of the second medium (n2) = 1.60
- Radius of curvature (R) = 20 cm (for a convex surface, R is positive)
- Object distance (u) = -200 cm (the object distance is negative as per the sign convention)
For a spherical refracting surface, the formula is given by:
−n1u+n2v=n2−n1R
Substituting the values we have:
−4/3−200+1.6v=1.6−4/320
Calculating the left side:
4/3200=4600=1150
So, we have:
1150+1.6v=1.6−1.333320
Calculating 1.6−1.3333:
1.6−1.3333=0.2667
Now substituting this into the equation:
1150+1.6v=0.266720
Calculating the right side:
0.266720=0.013335
Now we have:
1.6v=0.013335−1150
Calculating 1150:
1150=0.0066667
So, substituting this value:
1.6v=0.013335−0.0066667=0.0066683
Now, rearranging gives:
v=1.60.0066683≈240.00 cm
The position of the image formed is approximately 240 cm from the refracting surface.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Reflection Of Light By Spherical Mirrors
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Refraction
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSERTION AND REASON
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTPS ENGLISHChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution
Knowledge Check
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
A concave spherical surface of radius of curvature 10cm separates two mediums X and Y of refractive indices 4/3 and 3/2 respectively. Centre of curvature of the surfaces lies in the medium X. An object is placed in medium X.
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionThe eye can be regarded as a single refracting surface is equal to that of cornea (7.8 mm). This surface separates two media of refractive indices 1 and 1.34. Calculate the distance from the refracting surface at which a parallel beam of light will come to focus.
View SolutionA denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
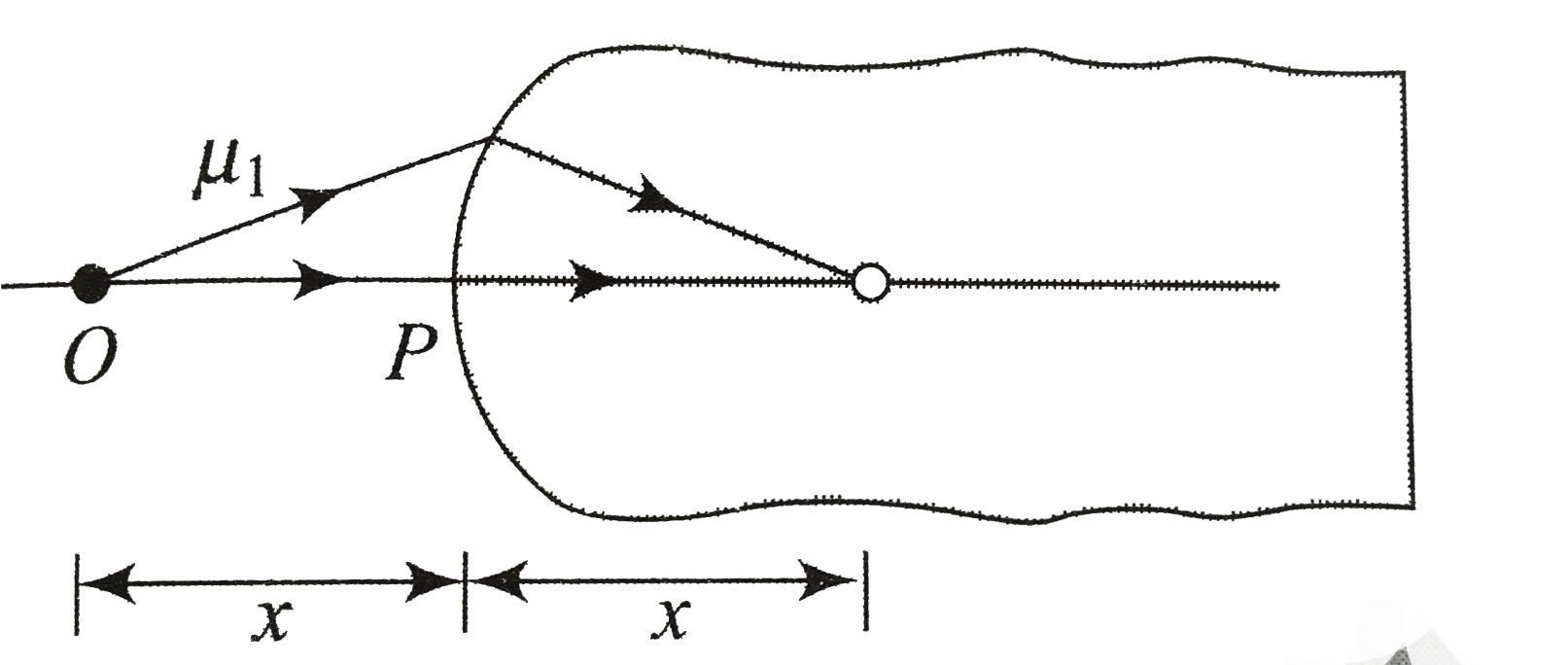
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionA concave spherical refractive surface with radius R separates a medium of refractive index 5/2 from air. As an object is approaching the surface from far away from the surface along the central axis, its image
View Solution