A boy of height 1m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is
0.25m
0.33m
0.5m
0.67m
The correct Answer is:C
To solve the problem step by step, we will use the concepts of ray optics, specifically the properties of convex mirrors.
Step 1: Identify the given information
- Height of the boy (object height, ho) = 1 m
- Distance of the boy from the mirror (object distance, u) = focal length of the convex mirror (let's denote it as f)
- Since the object is in front of the mirror, we take u=−f (the negative sign indicates that the object is in front of the mirror).
Hint: Remember that in optics, distances measured in the direction of the incident light are negative.
Step 2: Use the mirror formula
The mirror formula for a convex mirror is given by:
1f=1v+1u
Where:
- f = focal length of the mirror
- v = image distance
- u = object distance
Substituting u=−f into the mirror formula:
1f=1v−1f
Step 3: Rearranging the formula
Rearranging the equation to find 1v:
1v=1f+1f=2f
Thus, we can find v:
v=f2
Hint: Make sure to keep track of the signs when substituting values into the mirror formula.
Step 4: Calculate the magnification
The magnification m of a mirror is given by the formula:
m=−hiho=vu
Substituting the values we have:
m=vu=f2−f=−12
Step 5: Find the height of the image
Using the magnification formula:
m=−hiho
We can rearrange it to find the height of the image hi:
hi=−m⋅ho
Substituting m=−12 and ho=1m:
hi=−(−12)⋅1=12m
Final Answer
The height of the image is 0.5m.
---
- Height of the boy (object height, ho) = 1 m
- Distance of the boy from the mirror (object distance, u) = focal length of the convex mirror (let's denote it as f)
- Since the object is in front of the mirror, we take u=−f (the negative sign indicates that the object is in front of the mirror).
The mirror formula for a convex mirror is given by:
1f=1v+1u
Where:
- f = focal length of the mirror
- v = image distance
- u = object distance
1f=1v−1f
Rearranging the equation to find 1v:
1v=1f+1f=2f
Thus, we can find v:
v=f2
The magnification m of a mirror is given by the formula:
m=−hiho=vu
Substituting the values we have:
m=vu=f2−f=−12
Using the magnification formula:
m=−hiho
We can rearrange it to find the height of the image hi:
hi=−m⋅ho
Substituting m=−12 and ho=1m:
hi=−(−12)⋅1=12m
The height of the image is 0.5m.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A point object O is placed at a distance of 15 cm from a convex lens L of focal length 10 cm as shown in figure below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object 0. Find the focal length of the convex mirror.
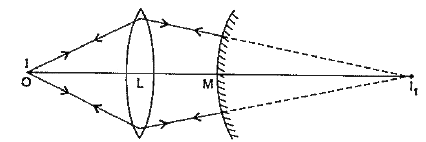
View SolutionThe distance of an object from a concave spherical mirror is equal to the focal length of the mirror. Then the image.
View SolutionAn object of length 4 cm is placed in front of a concave mirror at distance 30 cm. The focal length of mirror is 15 cm. a. Where will the image form? B. What will be the length of image?
View SolutionAn object is placed in front of a convex mirror at a distance of 50cm. A plane mirror is introduced covering the lower half of the convex mirror. If the distance between the object and the plane mirror is 30cm, it is found that there is no parallax between the images formed by the two mirrors. What is the radius of curvature of the convex mirror?
View SolutionA point light source is kept in front of a convex mirror at a distance of 40 cm. The focal length of the mirror is 40 cm. Find the position of image.
View SolutionA pole of height 4 m is kept in front of a vertical plane mirror
of length 2m. The lower end of the mirror is at a height of 6m form the grown
.the horizontal distance betweem the mirror and the pole is 2m. Upto what
minimum and maximum heights a man can see the image of top of the pole at a
horizontal distance of 4m (from the mirror O standing on the same horizontal
line which is passing through the pole and the horizontal point below the
mirror?

View SolutionThe image by a convex mirror is always formed in front of the mirror.
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View SolutionA person AB of height 170 cm is standing in front of a plane mirror. His eyes are at height 164 cm. At what distance from P should a hole be made in mirror so that he cannot see his hair?

View SolutionA man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of man from the mirror?
View Solution
