An object 2cm high is placed at a distance of 16cm from a concave mirror, which produces a real image 3cm high. What is thr focal length of the mirror ? Find the position of the image ?
−9.6cm
−3.6cm
−6.3cm
−8.3cm
The correct Answer is:A
To solve the problem step by step, we will use the mirror formula and the magnification formula for concave mirrors.
Step 1: Identify the given values
- Height of the object (h1) = 2 cm
- Height of the image (h2) = -3 cm (negative because the image is real)
- Object distance (u) = -16 cm (negative as per the sign convention for concave mirrors)
Step 2: Use the magnification formula
The magnification (m) is given by the formula:
m=h2h1=−vu
Substituting the known values:
m=−32
Step 3: Relate magnification to image distance (v)
From the magnification formula, we can express v in terms of u:
−vu=−32
v=32⋅u
Substituting u = -16 cm:
v=32⋅(−16)
v=−24cm
Step 4: Calculate the focal length using the mirror formula
The mirror formula is given by:
1f=1v+1u
Substituting the values of v and u:
1f=1−24+1−16
Finding a common denominator (48):
1f=−248+−348
1f=−548
Step 5: Solve for focal length (f)
Taking the reciprocal:
f=−485
f=−9.6cm
Step 6: Summary of results
- The focal length of the concave mirror is -9.6 cm.
- The position of the image is -24 cm (indicating that the image is formed on the same side as the object).
- Height of the object (h1) = 2 cm
- Height of the image (h2) = -3 cm (negative because the image is real)
- Object distance (u) = -16 cm (negative as per the sign convention for concave mirrors)
The magnification (m) is given by the formula:
m=h2h1=−vu
m=−32
From the magnification formula, we can express v in terms of u:
−vu=−32
v=32⋅u
v=32⋅(−16)
v=−24cm
The mirror formula is given by:
1f=1v+1u
1f=1−24+1−16
1f=−248+−348
1f=−548
Taking the reciprocal:
f=−485
f=−9.6cm
- The focal length of the concave mirror is -9.6 cm.
- The position of the image is -24 cm (indicating that the image is formed on the same side as the object).
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Reflection Of Light By Spherical Mirrors
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Refraction
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSERTION AND REASON
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTPS ENGLISHChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
An object 2.5 cm high is placed at a distance of 10 cm from a concave mirror of radius of curvature 30 cm The size of the image is
View SolutionFor an object placed at a distance 20 cm from a concave mirror, the image is formed at the same position. What is the focal length of the mirror?
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionAn object placed at 20cm in front of a concave mirror produces three times magnified real image. What is the focal length of the concave mirror?
View SolutionAn object 4cm in size is placed at a distance of 25.0cm from a concave mirror of focal length 15.0 cm. Find the position, nature and height of the image.
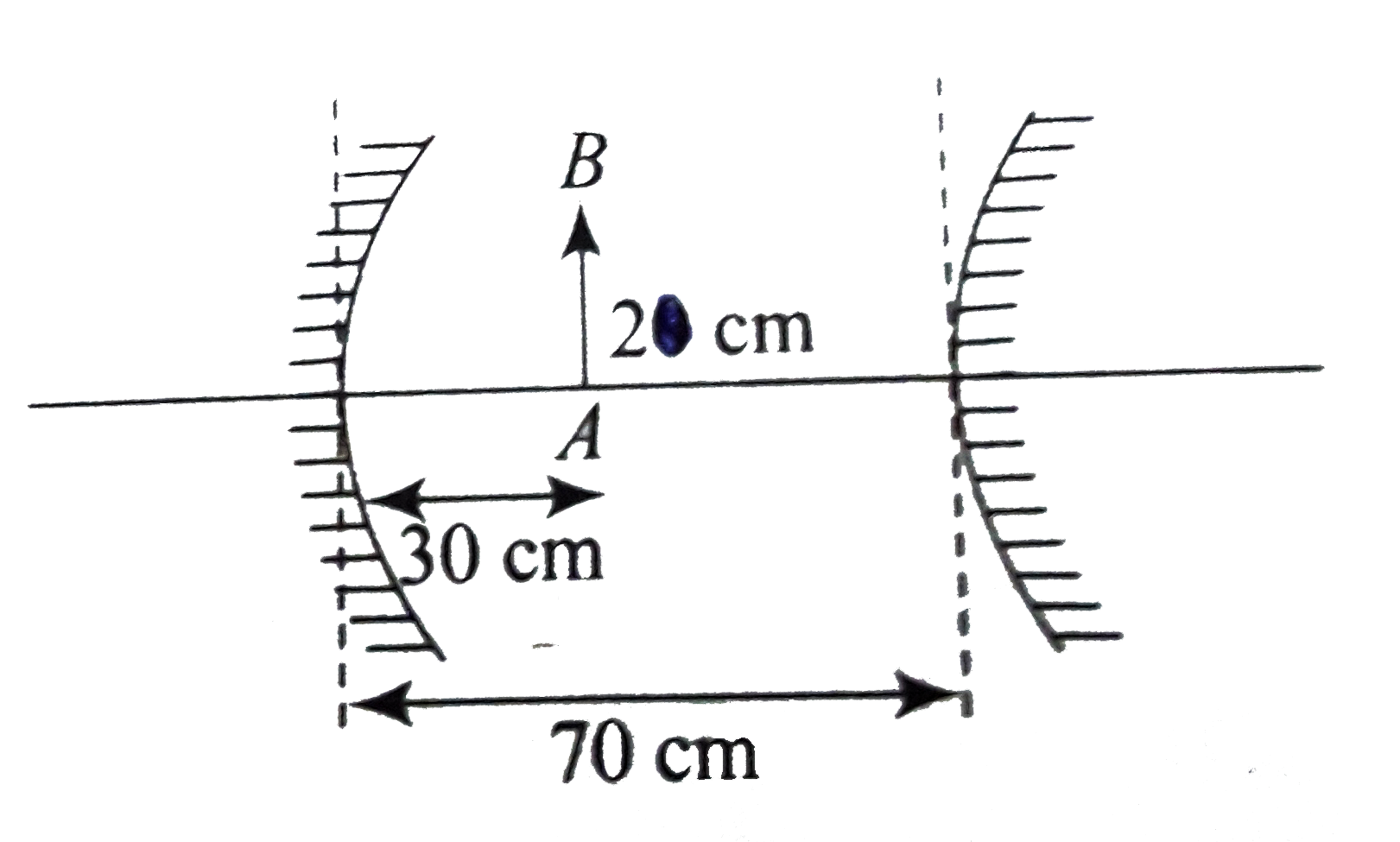
View SolutionA concave mirror and a convex mirror of focal lengths 10cm and 15cm are places at a distance of 70cm. An object AB of height 2cm is places at a distance of 30cm from the concave mirror. First ray is incident on the concave mirror then on the convex mirror. Find size, position, and nature of the image.
View SolutionAn object 5 cm high is placed at a distance 60 cm in fornt of a concave mirror of focal length 10 cm. Find (i) the position and (ii) size, of the image.
View SolutionA point object is placed at distance of 30 cm in front of a convex mirror of Focal length 30 cm. The image will form at
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View Solution

